Hiểu đơn giản, nó là kỹ thuật sử dụng 2 điểm di động để thực hiện mục đích nào đấy dựa vào yêu cầu các bài toán.
Một số bài toán đơn giản sử dụng two pointer:
Bài I:
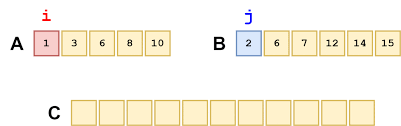
Đề bài: Cho hai dãy tăng dần a và b. Hãy ghép chúng thành một dãy c cũng có thứ tự tăng dần
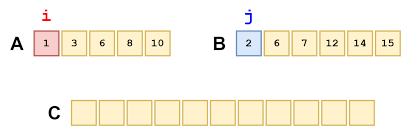
Hướng dẫn:
- Khởi tạo 2 điểm i và j bằng 1 chính là số thứ tự của 2 phần tử bé nhất của dãy a và dãy b.
- Mỗi bước mình sẽ so sánh a[i] và b[j], phần tử nào bé hơn thì sẽ là phần tử tiếp theo của dãy c.
- Cứ lặp lại như thế cho đến khi dãy c được hoàn thành.
Hai điểm i và j trong bài này chính là một ví dụ đơn giản cho kỹ thuật two pointer.
Bài II:
Đề bài: Cho dãy a tăng dần và một số x. Tìm 2 vị trí i và j sao cho a[i] + a[j] = x.
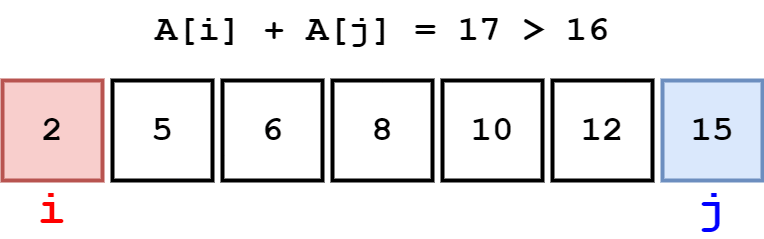
Hướng dẫn:
- Ta có các nhận xét như sau:
- Gọi n là độ dài dãy a, khởi tạo i = 1 và j = n:
- Nếu a[i] + a[j] > x thì bắt buộc phải giảm j xuống để tiếp tục so sánh vs x vì dãy a là dãy tăng dần, nếu i tăng lên thì a[i] + a[j] cũng sẽ tăng.
- Nếu a[i] + a[j] < x thì phải tăng i lên để tổng a[i] + a[j] tăng lên
- Vì sao i phải tăng và j phải giảm, bởi vì 2 trường hợp trên đã loại đi các trường hợp i giảm và j tăng.
- Gọi n là độ dài dãy a, khởi tạo i = 1 và j = n:
- Chúng ta sẽ chứng minh bằng phương pháp phản chứng:
- Giả sử hiện tại có i và j, a[i] + a[j] < x:
- Có 2 khả năng để tăng a[i] + a[j] lên là tăng i và tăng j. Bây giờ mình sẽ chứng minh vì sao không tăng i được.
- Giả sử: a[i] + a[j+1] = x .
- Vì a là dãy tăng dần nên a[1] ≤ a[2] ≤ … ≤ a[i]
- Chính vì thế, a[1] + a[j+1] ≤ x, tương tự a[2], … , a[i-1] cũng thế.
- Vì ≤ x nên lúc đó mình sẽ tăng i lên chứ không bao giờ giảm j xuống, vậy nên không có chuyện point j giảm xuống giá trị j hiện tại mà vẫn phải nằm ở j + 1. Vậy nên, nếu đã xuống giá trị j hiện tại thì chứng tỏ a[j + 1] + a[t] > x (t < i).
- Giả sử hiện tại có i và j, a[i] + a[j] < x:
Tóm tắt phương pháp:
- Khởi tạo 2 điểm two pointer i = 1, j = n:
Lặp lại liên tục các bước sau đến khi tìm được kết quả:
- Nếu a[i] + a[j] == x thì rút ra kq
- Nếu a[i] + a[j] > x thì giảm j
- Nếu a[i] + a[j] < x thì tăng i
Bài III:
Đề bài: Cho dãy a chứa n kí tự từ a – z. Tìm đoạn dài nhất mà các phần tử trong đoạn riêng biệt
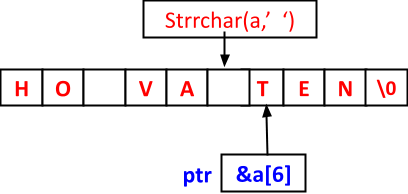
Hướng dẫn:
- Bài toán này tiếp tục khởi tạo 2 điểm two pointer i và j bắt đầu là 1.
- Trong bài này, điểm i là điểm bắt đầu, j sẽ đóng vai trò của điểm kết thúc.
- Với mỗi i, chúng ta có thể tìm được một j xa i nhất sao cho dãy đó là một đoạn riêng biệt.
Hãy cùng đoán xem độ phức tạp của thuật toán này là bao nhiêu? O(n^2). Mọi người có thể nhìn qua và suy đoán được như vậy. Thực tế khi sử dụng kỹ thuật này, độ phức tạp giảm chỉ còn O(2*n) mà tổng quát là O(n).
Giải thích:
- Gọi jk là j xa ik nhất tìm được như trên.
- Vì sao độ phức tạp chỉ có O(n), vì i tăng dần thì j cũng tăng dần, khi i tăng lên, ta chỉ cần kế thừa j của i trước đó để tiếp tục tăng lên. Trong suốt quá trình chạy của 2 điểm i và j, cả 2 đều độc lập chạy từ 1 -> n => độ phức tạp chỉ còn O(n).
Trên đây là một số bài toán sử dụng kỹ thuật two pointer, một kỹ thuật khá là linh hoạt, có thể ứng dụng với nhiều bài toán.


