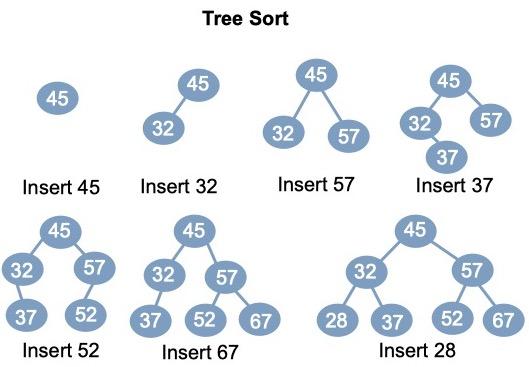
Tree Sort: Hiểu về thuật toán sắp xếp Cây

Tree sort là một thuật toán sắp xếp dựa trên cấu trúc dữ liệu cây, thường là cây nhị phân. Thuật toán này hoạt động bằng cách chèn các phần tử vào cây theo thứ tự, sau đó duyệt cây theo thứ tự inorder để trích xuất các phần tử đã được sắp xếp.

1. Cách hoạt động của thuật toán Tree Sort

Giả sử ta có mảng cần sắp xếp arr = [5, 3, 7, 2, 4, 6, 8]

Bước 1: Tạo mảng đếm

Chèn phần tử:

Bắt đầu với phần tử đầu tiên 5 và đặt nó làm gốc (root) của cây.
Chèn 3: nhỏ hơn 5, đặt làm con trái của 5.
Chèn 7: lớn hơn 5, đặt làm con phải của 5.
Chèn 2: nhỏ hơn 5, nhỏ hơn 3, đặt làm con trái của 3.
Chèn 4: nhỏ hơn 5, lớn hơn 3, đặt làm con phải của 3.
Chèn 6: lớn hơn 5, nhỏ hơn 7, đặt làm con trái của 7.
Chèn 8: lớn hơn 5, lớn hơn 7, đặt làm con phải của 7.

Bước 2: Duyệt cây theo thứ tự trung vị

Duyệt cây theo thứ tự trung vị (in-order traversal) nghĩa là duyệt cây theo thứ tự: trái, gốc, phải.
Bắt đầu từ gốc 5, ta đi tới con trái 3, tiếp tục đi tới con trái 2. 2 không có con, ta thu thập 2.
Quay lại 3, thu thập 3, đi tới con phải 4, thu thập 4.
Quay lại gốc 5, thu thập 5, đi tới con phải 7, tiếp tục tới con trái 6, thu thập 6.
Quay lại 7, thu thập 7, đi tới con phải 8, thu thập 8.

Kết quả là mảng đã được sắp xếp: [2, 3, 4, 5, 6, 7, 8]

2. Code thuật toán Tree Sort

class Node {
    constructor(data) {
        this.data = data;
        this.left = null;
        this.right = null;
    }
}

class BinarySearchTree {
    constructor() {
        this.root = null;
    }

    insert(data) {
        const newNode = new Node(data);
        if (this.root === null) {
            this.root = newNode;
        } else {
            this.insertNode(this.root, newNode);
        }
    }

    insertNode(node, newNode) {
        if (newNode.data < node.data) {
            if (node.left === null) {
                node.left = newNode;
            } else {
                this.insertNode(node.left, newNode);
            }
        } else {
            if (node.right === null) {
                node.right = newNode;
            } else {
                this.insertNode(node.right, newNode);
            }
        }
    }

    inOrderTraverse(node, result) {
        if (node !== null) {
            this.inOrderTraverse(node.left, result);
            result.push(node.data);
            this.inOrderTraverse(node.right, result);
        }
    }

    getSortedArray() {
        const result = [];
        this.inOrderTraverse(this.root, result);
        return result;
    }
}

function treeSort(arr) {
    const bst = new BinarySearchTree();
    for (let i = 0; i < arr.length; i++) {
        bst.insert(arr[i]);
    }
    return bst.getSortedArray();
}

// Example usage:
let arr = [5, 3, 7, 2, 4, 6, 8];
console.log("Original array:", arr);
arr = treeSort(arr);
console.log("Sorted array:", arr);

3. Phân tích độ phức tạp của thuật toán Tree Sort

Độ phức tạp về thời gian của trường hợp trung bình: O(n log n) Việc thêm một mục vào cây Tìm kiếm nhị phân trung bình mất O(log n) thời gian. Do đó, việc thêm n mục sẽ mất thời gian O(n log n)

Độ phức tạp thời gian trong trường hợp xấu nhất: O(n ² ). Độ phức tạp về thời gian trong trường hợp xấu nhất của Tree sort có thể được cải thiện bằng cách sử dụng cây tìm kiếm nhị phân tự cân bằng như Cây đen đỏ, Cây AVL. Sử dụng cây nhị phân tự cân bằng Tree Sort sẽ mất thời gian O(n log n) để sắp xếp mảng trong trường hợp xấu nhất.

Không gian phụ trợ: O(n)

4. Ưu và nhược điểm của Tree Sort

4.1 Ưu điểm

Độ Phức Tạp Thời Gian Trung Bình Tốt:
- Tree Sort có độ phức tạp thời gian trung bình là O(n log n), tương đương với các thuật toán sắp xếp hiệu quả khác như Merge Sort và Quick Sort.
Sắp Xếp Ổn Định:
- Nếu được triển khai chính xác với cây nhị phân tìm kiếm, Tree Sort có thể là thuật toán sắp xếp ổn định, giữ nguyên thứ tự của các phần tử có giá trị bằng nhau.
Khả Năng Cập Nhật Liên Tục:
- Tree Sort cho phép chèn và xóa phần tử trong khi duy trì thứ tự đã sắp xếp, làm cho nó phù hợp với các ứng dụng mà dữ liệu cần được cập nhật liên tục.
Sử Dụng Hiệu Quả Cây Nhị Phân Tìm Kiếm:
- Tree Sort khai thác hiệu quả cây nhị phân tìm kiếm để thực hiện các thao tác chèn và duyệt, giúp dễ dàng hiểu và triển khai.
Không Yêu Cầu Bộ Nhớ Bổ Sung Đáng Kể:
- Tree Sort không yêu cầu nhiều bộ nhớ bổ sung ngoài không gian dành cho cây nhị phân tìm kiếm, đặc biệt khi so sánh với Merge Sort, cần không gian bổ sung cho mảng tạm thời.

4.2 Nhược điểm

Trường Hợp Tệ Nhất:
- Trong trường hợp tệ nhất, khi cây nhị phân tìm kiếm trở thành cây thẳng (degenerate tree), độ phức tạp thời gian của Tree Sort trở thành O(n^2). Điều này xảy ra khi các phần tử được chèn vào cây theo thứ tự tăng dần hoặc giảm dần.
Yêu Cầu Cân Bằng Cây:
- Để đạt hiệu suất tốt nhất, cây nhị phân tìm kiếm cần được cân bằng. Việc duy trì một cây cân bằng có thể đòi hỏi các kỹ thuật phức tạp hơn như cây AVL hoặc cây đỏ-đen, làm tăng độ phức tạp của triển khai.
Hiệu Suất Không Nhất Quán:
- Tree Sort có thể không nhất quán về hiệu suất tùy thuộc vào cách các phần tử được phân phối ban đầu. Điều này làm cho nó ít dự đoán được so với các thuật toán khác như Merge Sort hoặc Quick Sort.
Chi Phí Bộ Nhớ cho Con Trỏ:
- Cây nhị phân tìm kiếm sử dụng nhiều con trỏ (left và right) cho mỗi nút, dẫn đến việc sử dụng bộ nhớ lớn hơn so với một số thuật toán sắp xếp khác như Quick Sort, đặc biệt khi số lượng phần tử lớn.
Không Phù Hợp Cho Dữ Liệu Trực Tuyến Lớn:
- Với dữ liệu trực tuyến (streaming data) hoặc dữ liệu rất lớn mà không thể chứa trong bộ nhớ, Tree Sort có thể không phù hợp do giới hạn bộ nhớ và khả năng xử lý.

5. Ứng dụng vào thực tế

Tree Sort được sử dụng trong các tình huống cần duy trì một tập hợp các phần tử được sắp xếp và hỗ trợ các thao tác chèn và tìm kiếm hiệu quả.

6. Kết luận

Tree Sort là một thuật toán sắp xếp hiệu quả với độ phức tạp thời gian trung bình là O(n log n). Tuy nhiên, để đạt được hiệu suất tốt nhất, cây nhị phân tìm kiếm cần được cân bằng. Trong trường hợp xấu nhất, Tree Sort có thể trở nên kém hiệu quả. Tree Sort thích hợp cho các ứng dụng mà dữ liệu được chèn và tìm kiếm liên tục trong một tập hợp đã sắp xếp.

7. Tài liệu tham khảo

Để hiểu hơn về thuật toán Tree Sort bạn có thể truy cập vào: https://www.geeksforgeeks.org/tree-sort/