Tổng quan về mật mã học trong Bitcoin

SECP256k1

Quay trở lại với Bitcoin, nó sử dụng đường cong SECP256k1 https://en.bitcoin.it/wiki/Secp256k1. Đường cong này có dạng:

y² = x³ + 7 (mod p)

và được xét trên một trường hữu hạn Fp, trong đó p là một số nguyên tố rất lớn, cụ thể là:

Ngoài ra, SECP256k1 còn xác định một điểm gọi là điểm cơ sở (base point), hay còn gọi là điểm sinh (generator point) — thường được ký hiệu là G, nằm trên đường cong này. Điểm này được dùng để tạo khóa công khai, phần sẽ được nói đến sau.

Ví dụ đơn giản: sử dụng Python để kiểm tra xem điểm G(x, y) có nằm trên đường cong SECP256k1 hay không:

>>> p = 115792089237316195423570985008687907853269984665640564039457584007908834671663
>>> x = 55066263022277343669578718895168534326250603453777594175500187360389116729240
>>> y = 32670510020758816978083085130507043184471273380659243275938904335757337482424
>>> (x ** 3 + 7) % p == y**2 % p
True

Phần lớn các hệ thống mã hóa dùng đường cong elliptic như P-256 (được NIST khuyến nghị) sử dụng tham số ngẫu nhiên có kiểm soát, nghĩa là được chọn một cách có mục đích để đạt một số thuộc tính nhất định.

SECP256k1 thì không như vậy — các tham số của nó rất “đơn giản” và không rõ là có được chọn ngẫu nhiên hay không, điều này dẫn đến mức độ tin tưởng cao hơn trong cộng đồng Bitcoin vì “không có cánh cửa sau” (backdoor) nghi ngờ từ chính phủ.

SECP256k1 vẫn đủ mạnh mẽ để bảo vệ Bitcoin trước các tấn công mật mã học hiện nay. Tính toán ngược từ khóa công khai về khóa riêng — tức giải bài toán logarit rời rạc trên đường cong elliptic (ECDLP) — là bất khả thi về mặt tính toán với công nghệ hiện tại.

Số điểm (kích thước nhóm) trên đường cong SECP256k1 là một số nguyên tố rất lớn, gần bằng 2^{256}. Điều này làm cho không gian khóa gần như vô tận — bạn có thể chọn ngẫu nhiên một số trong khoảng từ 1 đến 2^{256}−1 làm khóa riêng và gần như chắc chắn không trùng với bất kỳ ai.

Chữ ký điện tử (Digital Signature)

Chữ ký điện tử (ĐT), hay Chữ ký điện tử mã hóa (ĐTMC), là một thành phần của tài liệu điện tử, được tạo ra bằng quá trình mã hóa thông tin sử dụng khóa riêng (private key). Nó cho phép:

Xác minh rằng nội dung không bị thay đổi từ lúc ký (tính toàn vẹn),
Xác định ai là người ký (tính xác thực),
Và nếu xác minh thành công, chứng minh rằng người ký không thể phủ nhận hành động của mình (tính không thể chối bỏ).

(Theo Wikipedia)

Ý tưởng tổng quan như sau: Giả sử Alice muốn chuyển 1 BTC cho Bob. Cô ấy tạo một thông điệp dạng:

{
  "from": "1FXySbm7jpJfHEJRjSNPPUqnpRTcSuS8aN",  // địa chỉ của Alice
  "to": "1Eqm3z1yu6D4Y1c1LXKqReqo1gvZNrmfvN",   // địa chỉ của Bob
  "amount": 1                                  // gửi 1 BTC
}

Sau đó, Alice dùng khóa riêng của mình (hiện có thể hiểu là một con số chỉ mình cô biết), băm thông điệp (hash), và sử dụng một hàm dạng sign_text(private_key, text). Kết quả là một chữ ký điện tử — trong ECDSA(Elliptic Curve Digital Signature Algorithm), đó là một cặp số nguyên, còn với các thuật toán khác có thể có định dạng khác nhau.

Tiếp theo, cô gửi cho mạng lưới: thông điệp gốc, chữ ký, và khóa công khai của mình.

Bất kỳ ai cũng có thể sử dụng bộ ba đó cùng với hàm validate_signature(public_key, signature, text) để kiểm tra xem đúng là chủ nhân của khóa riêng đã ký thông điệp hay không. Và nếu cả mạng lưới đều biết khóa công khai đó thuộc về Alice, họ sẽ biết chính cô là người gửi — chứ không phải ai đó giả danh.

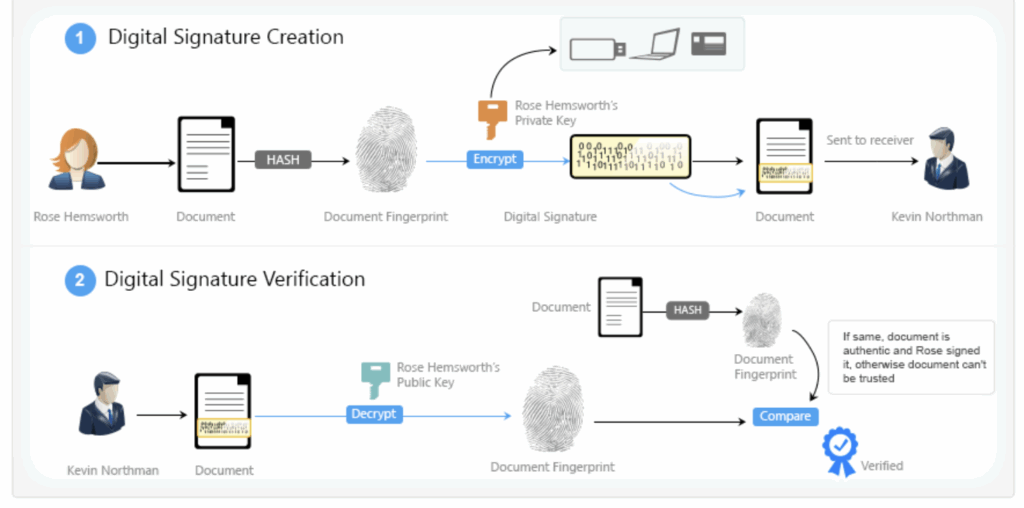
Giả sử có người tấn công

Giả sử có ai đó chen ngang giữa Alice và mạng lưới. Người này chặn thông điệp và thay đổi một chút — chỉ 1 bit trong cả tỷ bit. Ngay cả như vậy, khi kiểm tra validate_signature(public_key, signature, text') (với text' là thông điệp đã bị sửa), chữ ký sẽ không còn hợp lệ.

Đây là một tính năng cực kỳ quan trọng của Bitcoin, vì mạng lưới của nó là phân tán. Ta không thể biết chính xác ai sẽ nhận được giao dịch yêu cầu chuyển 1000 BTC. Nhưng họ không thể sửa đổi (ví dụ thay đổi người nhận thành địa chỉ của họ), vì giao dịch được ký bằng khóa riêng của bạn, và mọi người trong mạng sẽ phát hiện ra có điều gì đó sai.

⚠️ CHÚ Ý! Trên thực tế, quy trình phức tạp hơn nhiều so với mô tả ở trên. Ở đây chỉ là ví dụ đơn giản nhằm giải thích chữ ký điện tử là gì và nó được dùng để làm gì. Thuật toán thực sự được mô tả trong chương “Bitcoin in a Nutshell — Transactions”.