https://habr.com/ru/articles/319868
Một trong những lý do mà Bitcoin tiếp tục thu hút nhiều sự chú ý là tính “toán học” đặc biệt của nó. Satoshi Nakamoto đã thành công trong việc tạo ra một hệ thống có khả năng hoạt động mà không cần sự tin tưởng giữa các thành viên của nó. Tất cả các tương tác đều dựa trên toán học nghiêm ngặt, không có yếu tố con người — đó mới là điểm cách mạng của ý tưởng, chứ không phải ở mạng ngang hàng, như nhiều người nghĩ.
Dưới đây, tôi sẽ cố gắng giải thích cho bạn những điều cơ bản nhất — đường cong elliptic, ECC, khóa riêng / khóa công khai và những thứ tương tự.
Trong Bitcoin, người ta sử dụng cái gọi là mã hóa đường cong elliptic (Elliptic curve cryptography, ECC). Nó dựa trên một hàm đặc biệt nào đó — đường cong elliptic (không nhầm với elip).
Đường cong elliptic
Đường cong elliptic trên trường K là một đường cong bậc ba không đặc biệt trên mặt phẳng dự phòng trên {\hat {K}} (phần mở rộng đại số của trường K), được xác định bởi phương trình bậc ba với các hệ số từ trường K và “điểm ở vô cực” — Wikipedia
Nếu nói một cách đơn giản, thì đường cong elip là một hàm số có vẻ ngoài khá đơn giản, thường được biểu diễn dưới dạng gọi là dạng Weierstrass: $y^{2}=x^{3}+ax+b$
Tùy thuộc vào các giá trị của các tham số a và b, đồ thị của hàm này có thể trông khác nhau:
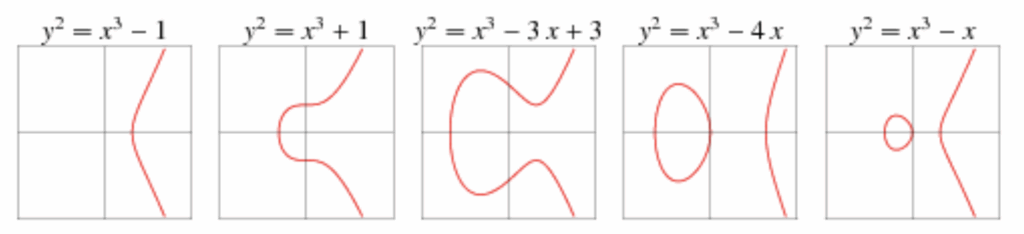
Bảng mã để vẽ đồ thị bằng Python:
import numpy as np
import matplotlib.pyplot as plt
def main():
a = -1
b = 1
y, x = np.ogrid[-5:5:100j, -5:5:100j]
plt.contour(x.ravel(), y.ravel(), pow(y, 2) - pow(x, 3) - x * a - b, [0])
plt.grid()
plt.show()
if __name__ == '__main__':
main()Nếu tin vào Wikipedia, thì lần đầu tiên hàm này xuất hiện trong các tác phẩm của Diophantus, và sau đó, vào thế kỷ 17, chính Newton cũng quan tâm đến nó. Nghiên cứu của ông đã dẫn đến nhiều công thức cộng các điểm trên đường cong ellip, mà chúng ta sẽ tìm hiểu ngay bây giờ. Ở đây và trong phần tiếp theo, chúng ta sẽ xem xét một số đường cong elliptic \alpha.
Giả sử có hai điểm P, Q ∈ α. Tổng của chúng được gọi là điểm R ∈ α, mà trong trường hợp đơn giản nhất được xác định như sau: vẽ một đường thẳng qua P và Q — nó sẽ cắt đường cong α tại một điểm duy nhất, gọi điểm đó là -R. Thay đổi tọa độ y của điểm -R thành đối diện về dấu, chúng ta sẽ có điểm R, mà chúng ta sẽ gọi là tổng của P và Q, tức là P + Q = R.
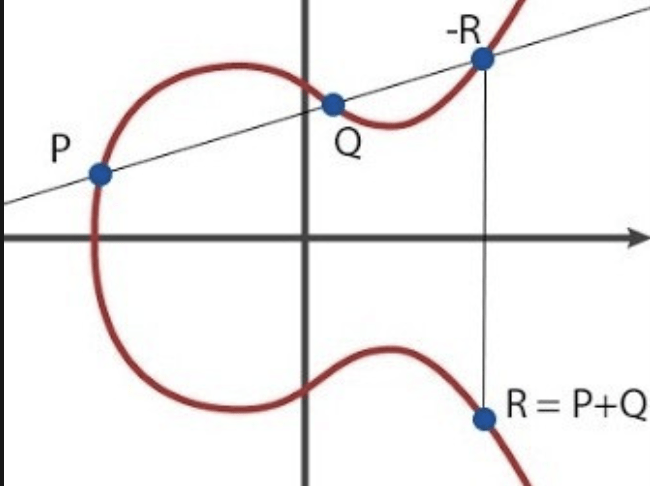
Tôi cho rằng cần lưu ý rằng chúng ta đang thực hiện phép cộng như vậy — nếu bạn cộng các điểm theo cách hiểu thông thường, tức là cộng các tọa độ tương ứng, thì bạn sẽ nhận được một điểm hoàn toàn khác R’ (x_1 + x_2, y_1 + y_2), mà có lẽ không có gì liên quan đến R hoặc -R và thậm chí không nằm trên đường cong \alpha.
Những người thông minh nhất đã tự hỏi — điều gì sẽ xảy ra nếu ví dụ như vẽ một đường thẳng qua hai điểm có tọa độ dạng P (a, b) và Q (a, -b), tức là đường thẳng đi qua chúng sẽ song song với trục tung (khung thứ ba trong hình dưới đây).
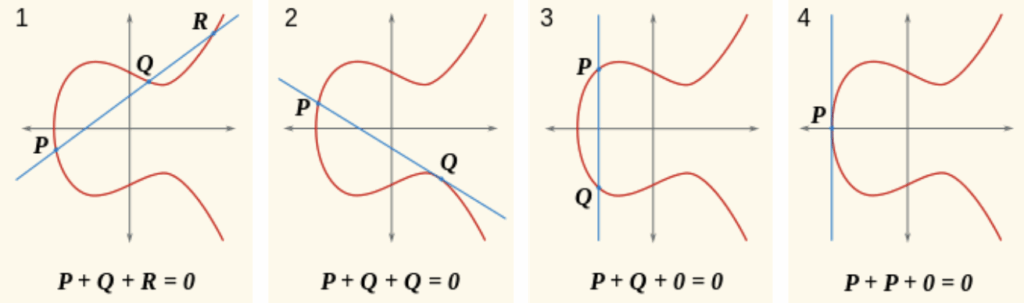
Không khó để thấy rằng trong trường hợp này không có giao điểm thứ ba với đường cong \alpha, mà chúng ta đã gọi là -R. Để tránh trường hợp này, chúng ta sẽ giới thiệu điểm vô cực (point of infinity), thường được ký hiệu là O hoặc đơn giản là , như trong hình. Và chúng ta sẽ nói rằng trong trường hợp không có giao điểm, P + Q = O.
Một trường hợp đặc biệt mà chúng tôi quan tâm là khi chúng tôi muốn cộng điểm với chính nó (khung 2, điểm Q). Trong trường hợp này, chúng tôi chỉ cần vẽ tiếp tuyến tại điểm Q và phản chiếu điểm giao nhau thu được qua trục y.
Bây giờ, với một động tác đơn giản, chúng ta có thể định nghĩa phép nhân một điểm với một số tự nhiên N. Kết quả là một điểm mới K=G⋅kK = G \cdot kK=G⋅k, tức là K=G+G+…+GK = G + G + \ldots + GK=G+G+…+G, lặp lại k lần. Khi nhìn vào hình minh họa thì mọi thứ sẽ trở nên rất rõ ràng.
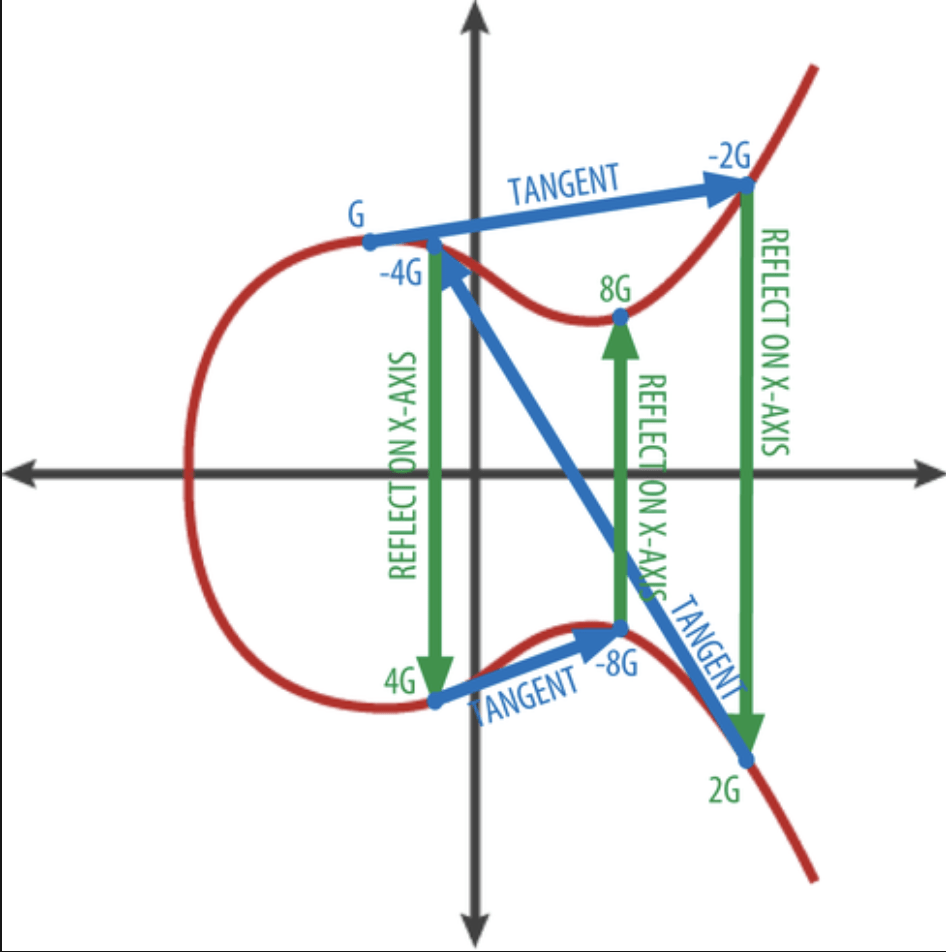
Đường cong elliptic trên trường hữu hạn
Trong lý thuyết ECC, sử dụng chính xác cùng một đường cong, chỉ khác là được xem xét trên một trường hữu hạn p là một số nguyên tố.
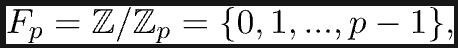
Nghĩa là:
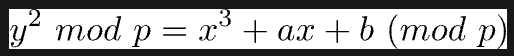
Tất cả các tính chất đã nêu (phép cộng, phép nhân, điểm ở vô cực) vẫn giữ nguyên đối với hàm số như vậy, mặc dù nếu cố gắng vẽ hàm số này thì nó sẽ chỉ hơi giống đường cong elliptic quen thuộc (trong trường hợp tốt nhất). Khái niệm ‘tiếp tuyến của hàm tại một điểm’ hoàn toàn mất đi ý nghĩa, nhưng điều đó không có gì nghiêm trọng. Dưới đây là một ví dụ về hàm số y^2 = x^3 + 7 trên trường hữu hạn với p=17:
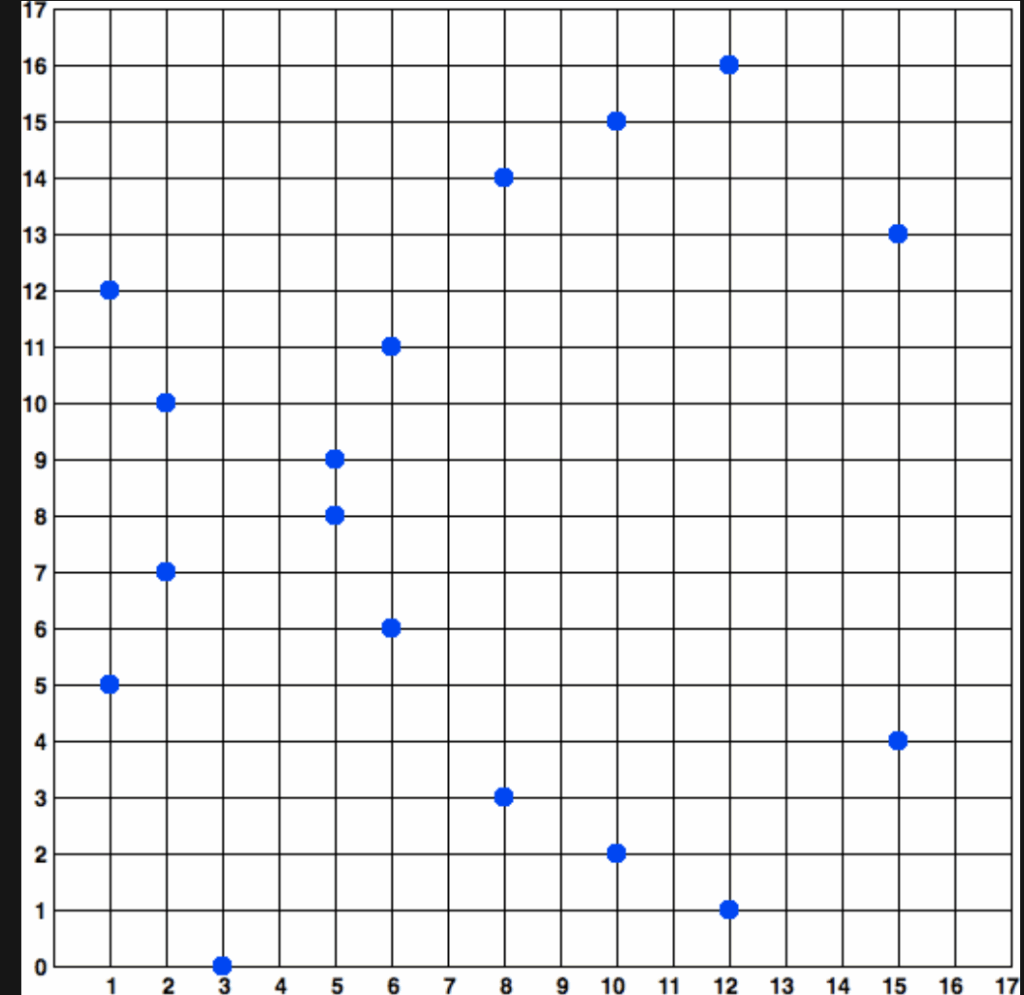
Còn với p = 59, thì ở đây gần như là một tập hợp điểm hỗn loạn. Điều duy nhất vẫn gợi nhớ đến nguồn gốc của đồ thị này là tính đối xứng qua trục hoành.
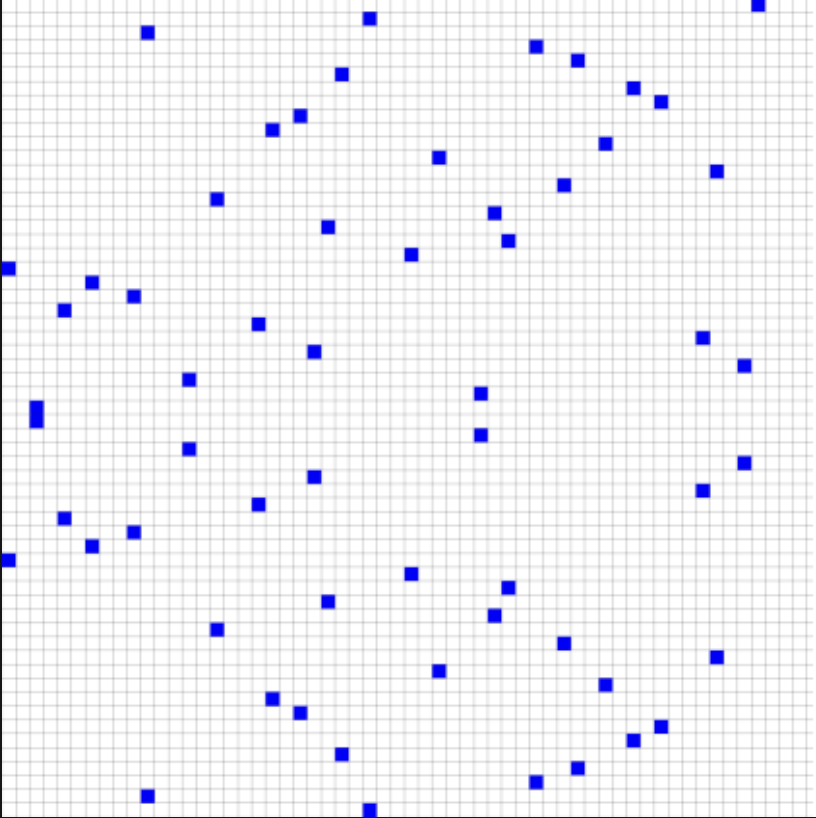
P.S. Nếu bạn quan tâm cách tính tọa độ điểm R(x₃, y₃) trên đường cong trên trường hữu hạn, khi đã biết tọa độ của hai điểm P(x₁, y₁) và Q(x₂, y₂) — bạn có thể xem qua cuốn “An Introduction to Bitcoin, Elliptic Curves and the Mathematics of ECDSA” của N. Mistry. Trong đó có giải thích rất chi tiết, và bạn chỉ cần kiến thức toán học ở trình độ lớp 8 là đủ để hiểu.
P.P.S. Trong trường hợp các ví dụ của tôi chưa làm thỏa mãn trí tò mò của bạn, đây là một trang web để vẽ các loại đường cong khác nhau — hãy thử tự mình khám phá nhé.
https://andrea.corbellini.name/ecc/interactive/modk-add.html



