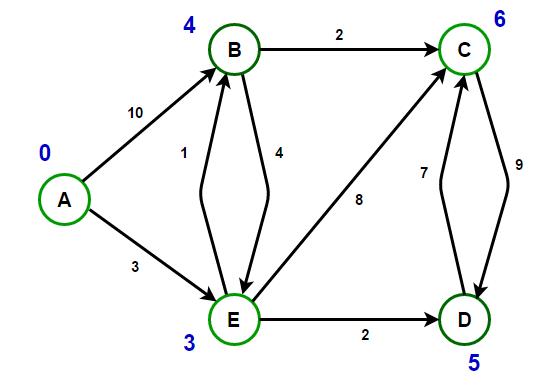
Thuật Toán Dijkstra – Tìm đường đi trong đồ thị

Thuật toán Dijkstra là một trong những thuật toán đồ thị nổi tiếng nhất, được sử dụng để tìm đường đi ngắn nhất từ một đỉnh nút gốc đến các đỉnh nút khác trong đồ thị có trọng số dương. Trong bài viết này, chúng ta sẽ cùng tìm hiểu về nguyên lý, cách triển khai, và ứng dụng của thuật toán Dijkstra.

1. Dijkstra là gì?

Thuật toán Dijkstra, do nhà khoa học máy tính Edsger Dijkstra phát minh năm 1956, được thiết kế để tìm đường đi ngắn nhất trong đồ thị hướng hoặc không hướng.

2. Nguyên lý hoạt động

Thuật toán hoạt động theo nguyên lý “tham lam” (greedy), liên tục chọn đường đi tối ưu tại mỗi bước. Các bước hoạt động của thuật toán như sau:

1. Khởi tạo:
   • Gán trọng số ban đầu cho tất cả các đỉnh nút là vô cùng (∞), trừ đỉnh nút gốc (gán trọng số là 0).
   • Tạo tập hợp các đỉnh nút chưa được duyệt.
2. Chọn đỉnh nút:
   • Tìm đỉnh nút trong tập chưa duyệt có trọng số nhỏ nhất.
3. Cập nhật:
   • Tính toán lại trọng số đến các đỉnh nút lân cận.
   • Nếu trọng số mới nhỏ hơn, cập nhật giá trị.
4. Lặp lại:
   • Loại bỏ đỉnh nút đã duyệt và lặp lại quá trình cho đến khi tất các đỉnh nút đã được duyệt.

3. Cài đặt thuật toán Dijkstra bằng Python

Dưới đây là mã giả minh họa cho thuật toán Dijkstra:

import heapq

def dijkstra(graph, start):
    # Khởi tạo bảng trọng số
    distances = {node: float('infinity') for node in graph}
    distances[start] = 0

    # Khởi tạo hàng đợi ưu tiên
    priority_queue = [(0, start)]

    while priority_queue:
        current_distance, current_node = heapq.heappop(priority_queue)

        # Bỏ qua nếu tốt nhất đã được xử lý
        if current_distance > distances[current_node]:
            continue

        # Cập nhật trọng số đến lân cận
        for neighbor, weight in graph[current_node].items():
            distance = current_distance + weight

            if distance < distances[neighbor]:
                distances[neighbor] = distance
                heapq.heappush(priority_queue, (distance, neighbor))

    return distances

# Ví dụ đồ thị
graph = {
    'A': {'B': 1, 'C': 4},
    'B': {'A': 1, 'C': 2, 'D': 6},
    'C': {'A': 4, 'B': 2, 'D': 3},
    'D': {'B': 6, 'C': 3}
}

start_node = 'A'
print(dijkstra(graph, start_node))

4. Phân tích độ phức tạp

• Độ phức tạp thời gian:
  • Sử dụng heap: O((V+E)log⁡V)O((V + E) \log V)
  • VV: Số đỉnh nút, EE: Số cạnh.
• Độ phức tạp không gian:
  • O(V)O(V) cho bảng trọng số và heap.

5. Ưu điểm và nhược điểm

• Ưu điểm:
  • Hiệu quả cao khi trọng số dương.
  • Cài đặt đơn giản, dễ hiểu.
• Nhược điểm:
  • Không hoạt động được với trọng số âm.
  • Độ phức tạp tăng ở đồ thị lơn.

6. Ưứng dụng trong thực tế

• Hệ thống GPS: Tìm đường đi ngắn nhất trong bản đồ giao thông.
• Mạng máy tính: Tìm đường truyền dữ liệu tối ưu.
• Lập kế hoạch tài nguyên: Tính toán chi phí vận chuyển tối thiểu.

7. Kết luận

Thuật toán Dijkstra là công cụ vô cùng hữu ích trong các bài toán tìm đường đi ngắn nhất. Nắm vữ cách triển khai và ứng dụng thuật toán này giúp bạn giải quyết nhiều bài toán thực tế một cách hiệu quả.