Giới thiệu về thuật toán tìm kiếm nhị phân
Bài toán quen thuộc về tìm kiếm nhị phân
Cho dãy số A có N phần tử, các phần tử trong dãy A đã được sắp xếp tăng dần (hoặc giảm dần), tức là A1 <= A2 <= ... AN-1 <= AN , và ta thường sẽ được yêu cầu thực hiện một trong các yêu cầu sau:
- Kiểm tra trong dãy có phần tử có giá trị X không? Nếu có trả về index, nếu không trả về -1
- Tìm phần tử có giá trị bé nhất và lớn hơn hoặc bằng X.
- Tìm phần tử có giá trị lớn nhất và nhỏ hơn hoặc bằng X.
Với cách Brute Force duyệt từ đầu cho đến cuối dãy để tìm ra phần tử thỏa mãn yêu cầu, ta có thể giải được với độ phức tạp là O(N) với mỗi yêu cầu tìm kiếm. Tuy nhiên nếu phải tìm kiếm nhiều lần như vậy thì ta cần có thuật toán hiệu quả hơn, tìm kiếm nhị phân là thuật toán tốt hơn cho trường hợp này với độ phức tạp O(logN) cho mỗi yêu cầu tìm kiếm.
Lời giải bằng thuật toán tìm kiếm nhị phân
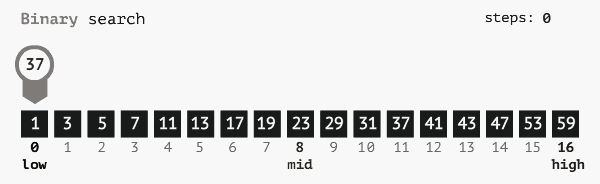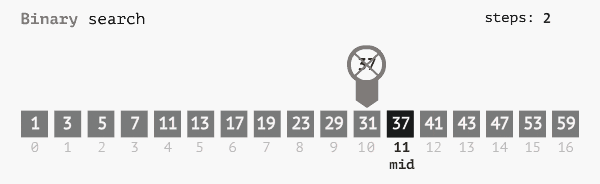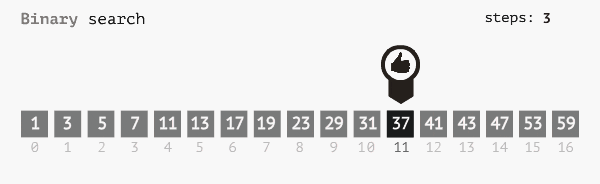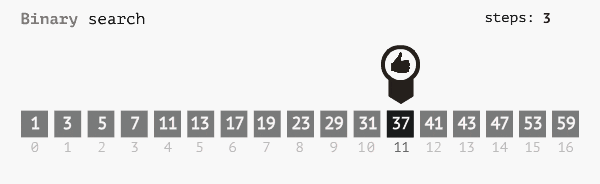
Thuật toán tìm kiếm nhị phân dựa vào tính chất tăng dần (hoặc giảm dần) của dãy số, để liên tục rút gọn phạm vi tìm kiếm sau mỗi lần so sánh phần tử ở giữa.
- Ta sẽ tìm kiếm biến X trên đoạn L, R, ban đầu ta sẽ gán
L = 0và R =N - 1 - Ta so sánh biến ở vị trí
mid = (L + R) / 2với X, dựa vào tính chất tăng dần của dãy số A ta có 3 trường hợp như sau:
1. Amid = X, tìm kiếm được mid là index của phần tử cần tìm
2. Amid < X, ta sẽ loại bỏ toàn bộ các phần từ đằng trước vị trímidra khỏi quá trình tìm kiếm, vì dãy A tăng dần nên các phần tử ở trướcmidsẽ lại càng bé hơn nữa => X sẽ có thể nằm trong đoạn từmid + 1 -> R, ta cập nhật lạiL = mid + 1để tiếp tục quá trình tìm kiếm ở bước sau.
3. Amid > X, lập luận tương tự ta cũng thấy rằng X chỉ có thể nằm đằng trước mid, tức là đoạn từL -> mid - 1, ta cập nhật lạiR = mid - 1để tiếp tục quá trình tìm kiếm. - Thuật toán kết thúc khi L > R tức là không tìm kiếm thấy phần tử X, return -1.
Trên đây là lời giải cho yêu cầu 1, bạn đọc có thể xem lời giải cho yêu cầu 2 và 3 tại Wikipedia
Code tham khảo
class Solution {
public int search(int[] nums, int target) {
int L = 0;
int R = nums.length - 1;
while (L <= R) {
int index = (L + R) / 2;
if (nums[index] == target) {
return index;
} else if (nums[index] > target) { // need bottom half
R = index - 1;
} else { // need top half
L = index + 1;
}
}
return -1;
}
}Đến đây thì anh em có thể “xơi” ngon mấy bài cơ bản về thuật toán tìm kiếm nhị phân trên leetcode rồi Binary Search
Thuật toán tìm kiếm nhị phân không chỉ có ứng dụng trong tìm kiếm phần tử trong dãy số, mà nó còn có ứng dụng với các bài tổng quát hơn.
Bài toán tổng quát
Cho số biến số x, và hàm số f(x), ta có thể áp dụng thuật toán tìm kiếm nhị phân với x thuộc đoạn [L,R] và hàm số f(x) có tính đơn điệu trên đoạn này, tính đơn điệu tức là:
- Đồng biến: x tăng thì f(x) cũng tăng, x giảm thì f(x) cũng giảm
- Nghịch biến: x giảm thì f(x) lại tăng, còn x tăng thì f(x) lại giảm
Ta cùng đi đến 1 ví dụ để hiểu rõ hơn bài toán tổng quát nhé.
Bài toán ví dụ
Có N kiện hàng trên 1 băng truyền phải được vận chuyển từ cảng này sang cảng khác trong thời gian không quá D ngày, kiện hàng thứi là Wi. Mỗi ngày, ta chất lên tàu các kiện hàng trên băng chuyền (theo thứ tự đã cho vì hàng trên băng truyền), và không được chất nhiều hơn trọng lượng hơn tối đa của tàu.
Hãy tìm trọng lượng bé nhất có thể của con tàu để vận chuyển N kiện hàng trong thời gian không quá D ngày.
Ràng buộc: N, D <= 105 , Wi <= 103
Ví dụ W = [1,2,3,4,5,6,7,8,9,10], D = 5. Kết quả 15
Giải thích:
- Ngày thứ 1: vận chuyển được 5 hàng đầu tiên có khối lượng 1, 2, 3, 4, 5
- Ngày thứ 2: vận chuyển được 2 hàng tiếp theo có khối lượng 6, 7
- Ngày thứ 3: vận chuyển được 1 hàng tiếp theo có khối lượng 8
- Ngày thứ 4: vận chuyển được 1 hàng tiếp theo có khối lượng 9
- Ngày thứ 5: vận chuyển được 2 hàng tiếp theo có khối lượng 10
Ý tưởng thuật toán
Ta có nhận xét đầu tiên là kết quả nằm trong đoạn [maxW, sumW] vì tàu phải lớn hơn khối lượng của hàng lớn nhất maxW để còn vẫn chuyển được maxW và trường hợp xấu nhất thì khối lượng của tàu sẽ phải là sumW để vận chuyển hết tất cả các hàng trong 1 ngày, gọi tắt đây là đoạn [L,R].
Xác định hàm số
Với 1 trọng lượng T nào đó của thuyền, ra sẽ tính được ra số ngày cần có để phải trở hết N kiện hàng và gọi đó là f(T), Bằng cách:
- Giả sử thuyền có tải trọng T, ban đầu khởi tạo ngày để vận chuyện hết được hàng hóa
currentDay = 1, và khối lượng hàng hóacurrentCapacity = 0. - Ta duyệt 1 vòng for O(N) từ đầu đến cuối của mảng W, thử nhét lần lượt hàng vào thuyền, nếu quá tải trọng thì sẽ tăng ngày
currentDayvà xétcurrentCapacity= khối lượng hàng hóa cần nhét vào. - Kết thúc vòng for
currentDaychính là kết quả cần tìm.
int currentDay = 1;
int currentCapacity = 0;
for (int weight : weights) {
if (currentCapacity + weight <= capacity) {
currentCapacity += weight;
} else {
currentDay++;
currentCapacity = weight;
}
}Nhận xét tính đơn điệu và ứng dụng tìm kiếm nhị phân
Nhận thấy T càng tăng thì f(T) sẽ càng giảm, vì trọng lượng thuyền tăng thì số ngày cần có để vận chuyên hết hàng sẽ càng ít đi.
Với một khối lượng T nào đó nếu tính ra f(T) > D => Với trọng lượng thuyền là T, cần nhiều số ngày hơn so với quy định là D ngày => Kết quả cần tìm sẽ phải lớn hơn T => kết quả cần tìm nằm trong đoạn [T+1, R].
Suy luận tương tự, với một khối lượng T nào đó nếu tính ra f(T) <= D, T có thể là một kết quả cần tìm, lưu lại T, và có thể có kết quả tốt hơn trong đoạn [L, T-1].
Và đây chính là tư tưởng dẫn dắt chúng ta đến thuật toán tìm kiếm nhị phân, ta luôn chọn T là giá trị giữa của [L,R], tức là (L + R)/2 để độ phức tạp tối ưu log(R-L).
Code tham khảo
class Solution {
public int shipWithinDays(int[] weights, int days) {
int maxCapacity = 0;
int maxWeight = 0;
for (int weight : weights) {
maxCapacity += weight;
if (weight > maxWeight) maxWeight = weight;
}
int minCapacity = maxWeight;
int result = maxCapacity;
int left = minCapacity, right = maxCapacity;
while (left <= right) {
int mid = left + (right-left)/2;
if (canShipPackages(weights, days, mid)) {
result = mid;
right = mid-1;
} else {
left = mid+1;
}
}
return result;
}
private boolean canShipPackages(int[] weights, int days, int capacity) {
int currentDay = 1;
int currentCapacity = 0;
for (int weight : weights) {
if (currentCapacity + weight <= capacity) {
currentCapacity += weight;
} else {
currentDay++;
currentCapacity = weight;
}
}
return currentDay <= days;
}
}




