Thuật toán cơ bản đến nâng cao #4: Stack và ứng dụng

1. Giới thiệu về cấu trúc dữ liệu Stack

Stack, hay còn gọi là ngăn xếp, là một cấu trúc dữ liệu tuyến tính hoạt động theo nguyên tắc LIFO (Last In, First Out), nghĩa là phần tử được thêm vào sau cùng sẽ được lấy ra đầu tiên. Cấu trúc này giống như một chồng đĩa: đĩa mới được đặt lên trên và khi cần lấy đĩa, ta sẽ lấy đĩa trên cùng trước. Stack thường được sử dụng trong nhiều thuật toán và quy trình xử lý dữ liệu vì tính đơn giản và hiệu quả của nó trong việc quản lý dữ liệu tạm thời.

Các thao tác cơ bản trên Stack

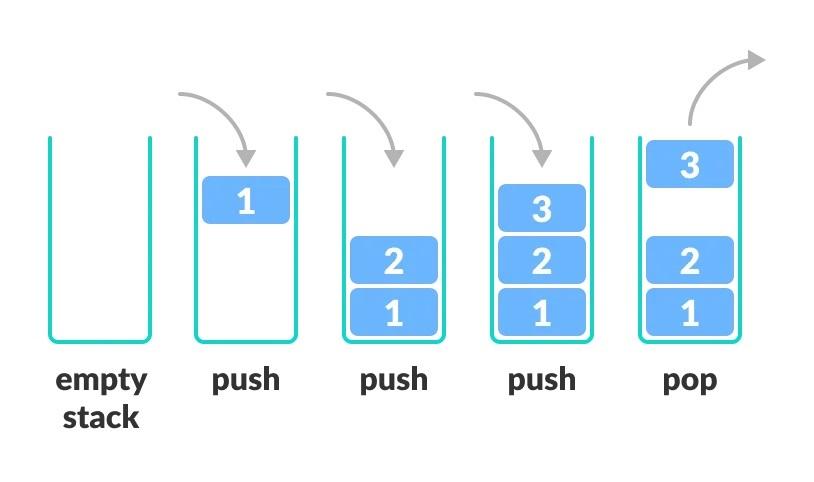
Push: Thêm một phần tử vào đầu Stack.
Pop: Lấy phần tử đầu tiên ra khỏi Stack.
Peek/Top: Truy cập phần tử đầu tiên mà không loại bỏ nó.
IsEmpty: Kiểm tra xem Stack có rỗng hay không.

Dưới đây là các thao tác cơ bản của một Stack và code minh họa bằng Python:

class Stack:
    def __init__(self):
        self.items = []

    def is_empty(self):
        return len(self.items) == 0

    def push(self, item):
        self.items.append(item)

    def pop(self):
        if not self.is_empty():
            return self.items.pop()
        else:
            raise IndexError("Pop from an empty stack")

    def peek(self):
        if not self.is_empty():
            return self.items[-1]
        else:
            raise IndexError("Peek from an empty stack")

    def size(self):
        return len(self.items)

Ví dụ về cách hoạt động của Stack

stack = Stack()
stack.push(1)
stack.push(2)
print(stack.peek())  # Output: 2
print(stack.pop())   # Output: 2
print(stack.peek())  # Output: 1
print(stack.is_empty())  # Output: False

Ban đầu, Stack rỗng: []
Thực hiện push(1): [1]
Thực hiện push(2): [1, 2]
Thực hiện pop(): [1] (phần tử 2 được lấy ra)
Thực hiện peek(): 1 (phần tử đầu tiên hiện tại là 1)

2. Ứng dụng của Stack có tính đơn điệu tăng dần, giảm dần trong thuật toán

Stack có tính đơn điệu, bao gồm đơn điệu tăng dần và đơn điệu giảm dần, là những Stack được duy trì theo cách mà các phần tử trong Stack luôn tuân theo một thứ tự nhất định. Các loại Stack này thường được sử dụng để giải quyết các bài toán phức tạp về cấu trúc dữ liệu và thuật toán.

Stack đơn điệu tăng dần

Stack đơn điệu tăng dần là Stack mà phần tử được thêm vào luôn nhỏ hơn hoặc bằng phần tử trước đó. Điều này có nghĩa là các phần tử trong Stack sẽ được sắp xếp theo thứ tự không giảm dần từ đáy lên đỉnh.

Tìm phần tử kế tiếp lớn hơn: Trong bài toán tìm phần tử kế tiếp lớn hơn của một mảng, Stack đơn điệu tăng dần giúp lưu trữ các phần tử chưa tìm được phần tử kế tiếp lớn hơn. Khi gặp phần tử lớn hơn, các phần tử trong Stack sẽ được cập nhật ngay lập tức.
Xử lý biểu thức toán học: Stack đơn điệu tăng dần có thể được sử dụng để tính toán biểu thức trung tố (infix) hoặc hậu tố (postfix) bằng cách đảm bảo các toán hạng được xử lý theo thứ tự đúng đắn.

Stack đơn điệu giảm dần

Stack đơn điệu giảm dần là Stack mà phần tử được thêm vào luôn lớn hơn hoặc bằng phần tử trước đó. Điều này có nghĩa là các phần tử trong Stack sẽ được sắp xếp theo thứ tự không tăng dần từ đáy lên đỉnh.

Tìm phần tử kế tiếp nhỏ hơn: Tương tự như bài toán tìm phần tử kế tiếp lớn hơn, nhưng Stack đơn điệu giảm dần được sử dụng để tìm phần tử kế tiếp nhỏ hơn trong một mảng.
Kiểm tra chuỗi ngoặc: Stack đơn điệu giảm dần có thể được sử dụng để kiểm tra tính hợp lệ của các chuỗi ngoặc bằng cách đảm bảo rằng mỗi ngoặc mở đều có ngoặc đóng tương ứng.

Nhờ vào đặc tính đơn giản nhưng mạnh mẽ của mình, Stack đơn điệu tăng dần và giảm dần trở thành công cụ hữu ích trong nhiều thuật toán và ứng dụng thực tế, giúp tối ưu hóa quá trình xử lý và quản lý dữ liệu một cách hiệu quả.

Cùng phân tích 1 bài toán sau để hiểu rõ hơn.

Phân tích bài toán: Tìm phần tử kế tiếp lớn hơn

Bài toán: Cho một mảng số nguyên, với mỗi phần tử, tìm phần tử đầu tiên lớn hơn nó ở bên phải. Nếu không có phần tử nào lớn hơn, trả về -1.

Giải pháp

Duyệt ngược qua mảng.
Sử dụng một Stack đơn điệu giảm dần để lưu trữ các phần tử.
Với mỗi phần tử, loại bỏ các phần tử nhỏ hơn hoặc bằng nó khỏi Stack.
Nếu Stack không rỗng, phần tử trên đỉnh Stack sẽ là phần tử lớn hơn kế tiếp. Nếu Stack rỗng, không có phần tử lớn hơn.

Code tham khảo

def next_greater_elements(nums):
    n = len(nums)
    result = [-1] * n
    stack = []

    for i in range(n - 1, -1, -1):
        while stack and stack[-1] <= nums[i]:
            stack.pop()
        if stack:
            result[i] = stack[-1]
        stack.append(nums[i])

    return result

# Ví dụ sử dụng
nums = [2, 1, 2, 4, 3]
print(next_greater_elements(nums))  # Output: [4, 2, 4, -1, -1]

3. Các ứng dụng khác của Stack trong thực tế

Stack được sử dụng rộng rãi trong nhiều ứng dụng và giải pháp thuật toán khác nhau. Dưới đây là một số ứng dụng tiêu biểu:

Đánh giá biểu thức toán học

Stack được sử dụng để đánh giá các biểu thức toán học dạng hậu tố (postfix) và tiền tố (prefix). Trong biểu thức trung tố (infix), Stack giúp quản lý các toán tử và toán hạng để đảm bảo thứ tự thực hiện đúng.

Quản lý đệ quy

Trong các ngôn ngữ lập trình, Stack được sử dụng để quản lý các cuộc gọi đệ quy. Mỗi cuộc gọi hàm mới sẽ được đẩy vào Stack, và khi hàm kết thúc, kết quả sẽ được lấy ra từ Stack.

Kiểm tra dấu ngoặc

Stack được sử dụng để kiểm tra tính hợp lệ của chuỗi ngoặc trong các biểu thức. Mỗi khi gặp một dấu ngoặc mở, nó được đẩy vào Stack. Khi gặp một dấu ngoặc đóng, dấu ngoặc mở tương ứng sẽ được lấy ra từ Stack để kiểm tra tính hợp lệ.

Duyệt cây (Tree Traversal)

Trong quá trình duyệt cây nhị phân theo phương pháp duyệt theo chiều sâu (Depth-First Search – DFS), Stack được sử dụng để lưu trữ các nút đang chờ được khám phá.

Undo và Redo

Trong các ứng dụng văn bản hoặc đồ họa, Stack được sử dụng để quản lý các thao tác undo (hoàn tác) và redo (làm lại). Mỗi thao tác được lưu vào Stack, và người dùng có thể hoàn tác hoặc làm lại các thao tác trước đó bằng cách lấy phần tử ra khỏi Stack.

Stack là một cấu trúc dữ liệu mạnh mẽ và linh hoạt, giúp giải quyết nhiều vấn đề thuật toán phức tạp một cách hiệu quả và tối ưu.