Thuật toán cơ bản đến nâng cao #3: Memoization trong đệ quy

1. Giới thiệu về kỹ thuật sử dụng bộ nhớ trong các thuật toán sử dụng đệ quy

Duyệt vét cạn

Duyệt vét cạn (brute force) là phương pháp tìm kiếm tất cả các lời giải có thể của một vấn đề bằng cách duyệt qua tất cả các khả năng. Tuy nhiên, do phải duyệt qua tất cả các khả năng, thời gian thực hiện của phương pháp này thường rất lâu, đặc biệt là với các bài toán có không gian tìm kiếm lớn.

Backtracking

Backtracking là một phương pháp cải tiến của duyệt vét cạn. Thay vì thử tất cả các khả năng, backtracking sẽ thử từng bước, và nếu một bước nào đó không khả thi, nó sẽ quay lui (backtrack) và thử bước tiếp theo. Kỹ thuật này giúp giảm số lượng các bước cần thử, nhưng với các bài toán phức tạp, vẫn có thể dẫn đến việc thử nhiều lần các bước tương tự nhau.

Kỹ thuật sử dụng bộ nhớ (Memoization)

Kỹ thuật memoization là một phương pháp tối ưu hóa trong lập trình, giúp giảm thời gian thực hiện của các thuật toán đệ quy bằng cách lưu trữ kết quả của các bài toán con đã được tính toán trước đó. Khi gặp lại một bài toán con đã được xử lý, thay vì tính lại, chúng ta chỉ cần lấy kết quả đã lưu từ bộ nhớ, giúp tiết kiệm thời gian và tài nguyên.

Để hiểu hơn về thuật toán này hãy cùng phân tích 1 bài toán ví dụ.

2. Bài toán ví dụ

Bài toán: Tìm đường đi ngắn nhất trên lưới (Grid)

Cho một lưới 𝑚×𝑛 với các ô chứa các giá trị dương, hãy tìm đường đi ngắn nhất từ ô trên cùng bên trái (0, 0) đến ô dưới cùng bên phải (m-1, n-1), sao cho tổng các giá trị trên đường đi là nhỏ nhất. Bạn chỉ có thể di chuyển xuống dưới hoặc sang phải.

Các hướng tiếp cận

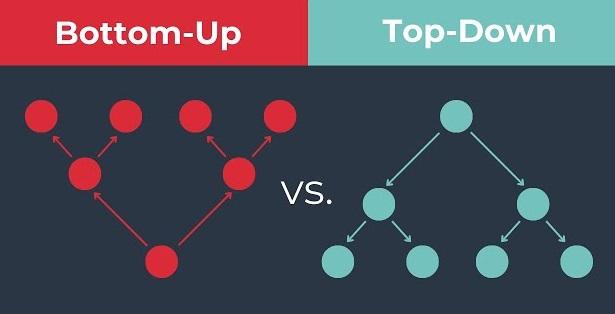
Cách tiếp cận Bottom-Up

Trong cách tiếp cận bottom-up, chúng ta xây dựng bảng kết quả từ dưới lên trên. Chúng ta khởi đầu từ ô cuối cùng và tính toán ngược lên ô đầu tiên bằng cách sử dụng một mảng hai chiều để lưu trữ kết quả tạm thời. Cách tiếp cận này thường được sử dụng trong lập trình động (dynamic programming).

Cách tiếp cận Top-Down

Trong cách tiếp cận top-down, chúng ta bắt đầu từ ô đầu tiên và sử dụng đệ quy để giải quyết bài toán bằng cách chia nhỏ nó thành các bài toán con. Kỹ thuật memoization được sử dụng để lưu trữ kết quả của các bài toán con đã tính toán, giúp tránh việc tính toán lại.

Giải pháp với cách tiếp cận Top-Down

Chúng ta sẽ sử dụng đệ quy và memoization để giải quyết bài toán này. Mỗi khi chúng ta tính toán đường đi ngắn nhất từ một ô cụ thể đến đích, chúng ta sẽ lưu kết quả vào bộ nhớ. Khi gặp lại ô này, chúng ta chỉ cần lấy kết quả từ bộ nhớ ra thay vì tính lại.

Code tham khảo

def minPathSum(grid):
    m, n = len(grid), len(grid[0])
    memo = {}

    def dfs(x, y):
        # Kiểm tra xem ô (x, y) đã được tính toán trước đó chưa
        if (x, y) in memo:
            return memo[(x, y)]
        # Nếu đạt đến ô cuối cùng, trả về giá trị của ô đó
        if x == m - 1 and y == n - 1:
            return grid[x][y]
        # Nếu vượt ra ngoài lưới, trả về vô cực để biểu thị đường này không hợp lệ
        if x >= m or y >= n:
            return float('inf')
        
        # Tính toán giá trị nhỏ nhất giữa việc di chuyển sang phải và di chuyển xuống dưới
        right = dfs(x, y + 1)
        down = dfs(x + 1, y)
        memo[(x, y)] = grid[x][y] + min(right, down)
        return memo[(x, y)]

    return dfs(0, 0)

# Ví dụ sử dụng
grid = [
    [1, 3, 1],
    [1, 5, 1],
    [4, 2, 1]
]
print(minPathSum(grid))  # Output: 7

Giải thích code

1. Khởi tạo: Chúng ta khởi tạo lưới và một dictionary memo để lưu trữ kết quả của các bài toán con.
2. Đệ quy với memoization: Hàm dfs (Depth-First Search) được sử dụng để duyệt qua các ô trong lưới. Tại mỗi ô (x, y), nếu nó đã được tính trước đó, chúng ta trả về kết quả đã lưu trong memo.
3. Điều kiện cơ bản: Nếu ô hiện tại là ô cuối cùng (m-1, n-1), chúng ta trả về giá trị của ô đó.
4. Điều kiện vượt lưới: Nếu ô hiện tại vượt ra ngoài lưới, chúng ta trả về vô cực (infinity) để biểu thị đường này không hợp lệ.
5. Tính toán giá trị nhỏ nhất: Chúng ta tính toán giá trị nhỏ nhất giữa ô bên phải và ô phía dưới, sau đó lưu kết quả vào memo.

Cách tiếp cận Top-Down

Cách tiếp cận top-down cho phép chúng ta giải quyết bài toán một cách tự nhiên bằng đệ quy, thông thường với các bài toán phức tạp và thuật toán giải dựa trên kết quả của bài toán con ta sẽ dễ nhìn ra hướng giải bằng phương pháp này hơn, vì cách tiếp cận top-down rất tự nhiên.

Đồng thời sử dụng memoization để lưu trữ kết quả của các bài toán con đã tính toán, giúp tối ưu hóa thời gian thực hiện.

Kỹ thuật này rất hữu ích cho các bài toán có nhiều bài toán con lặp lại, giảm thiểu số lần tính toán lại và tăng hiệu quả của thuật toán.

3. Ứng dụng xa hơn của thuật toán này trong thực tế

Ứng dụng trong các bài toán tối ưu hoá

Memoization thường được sử dụng trong các bài toán tối ưu hóa như bài toán cái túi (Knapsack problem), bài toán chuỗi con chung dài nhất (Longest Common Subsequence), và các bài toán liên quan đến tìm đường trong đồ thị (Graph).

Ứng dụng trong xử lý chuỗi và đồ thị

Các bài toán về xử lý chuỗi như tìm chuỗi con dài nhất, kiểm tra chuỗi con cũng có thể được tối ưu bằng memoization. Trong xử lý đồ thị, memoization giúp tăng hiệu quả của các thuật toán tìm kiếm như DFS và BFS khi chúng ta cần tính toán lại các đường đi hoặc chi phí.

Ứng dụng trong trí tuệ nhân tạo và học máy

Trong AI và Machine Learning, memoization có thể được sử dụng để lưu trữ kết quả của các mô hình huấn luyện trung gian, giúp giảm thời gian huấn luyện và tối ưu hóa các thuật toán học máy.

Kết luận

Kỹ thuật memoization không chỉ giúp tăng hiệu quả của các thuật toán đệ quy, backtracking mà còn mở ra nhiều ứng dụng trong các lĩnh vực khác nhau, từ tối ưu hóa đến xử lý chuỗi và đồ thị, cũng như trong AI và học máy. Bằng cách lưu trữ kết quả của các bài toán con, chúng ta có thể giảm thiểu thời gian tính toán và tài nguyên, giúp các giải pháp trở nên hiệu quả hơn.