Thuật toán A* (A-star) là một trong những thuật toán tìm kiếm đường đi ngắn nhất phổ biến và hiệu quả nhất. Nó được sử dụng rộng rãi trong lập trình game, định tuyến GPS và nhiều ứng dụng khác trong lĩnh vực trí tuệ nhân tạo và robot.
1. Giới Thiệu Về A*
A* là một thuật toán tìm kiếm theo cơ chế heuristic, tức là nó sử dụng thông tin dự đoán để hướng dẫn quá trình tìm kiếm. Thuật toán này kết hợp giữa tìm kiếm theo chi phí thấp nhất (like Dijkstra) và tìm kiếm theo chiều sâu (depth-first search), giúp tìm ra đường đi ngắn nhất một cách nhanh chóng.
2. Cách A* Hoạt Động

A* hoạt động bằng cách mở rộng các nút (điểm) từ điểm bắt đầu đến điểm kết thúc dựa trên hàm đánh giá 𝑓(𝑛). Hàm này kết hợp giữa chi phí đi từ điểm bắt đầu đến điểm hiện tại (𝑔(𝑛)) và ước lượng chi phí từ điểm hiện tại đến điểm đích (ℎ(𝑛)):
𝑓(𝑛) = 𝑔(𝑛) + ℎ(𝑛)
- 𝑔(𝑛): Chi phí từ điểm bắt đầu đến điểm hiện tại.
- ℎ(𝑛): Hàm heuristic ước lượng chi phí từ điểm hiện tại đến điểm đích.
3. Các Bước Của Thuật Toán A*
Khởi Tạo
- Đặt điểm bắt đầu vào danh sách mở (open list) và gán giá trị 𝑓 ban đầu cho nó.
- Đặt danh sách đóng (closed list) rỗng.
Lặp Lại
- Chọn nút trong danh sách mở có giá trị 𝑓 nhỏ nhất và di chuyển nó sang danh sách đóng.
- Nếu nút này là điểm đích, thì đường đi ngắn nhất đã được tìm thấy.
- Nếu không, đối với mỗi nút kề cận:
- Tính giá trị 𝑔 và 𝑓 cho nút kề.
- Nếu nút này chưa có trong danh sách mở hoặc có giá trị 𝑓 nhỏ hơn giá trị hiện tại trong danh sách mở, thì cập nhật giá trị và đặt nút này vào danh sách mở.
Kết Thúc
- Lặp lại quá trình cho đến khi tìm thấy điểm đích hoặc danh sách mở rỗng (đường đi không tồn tại).
4. Ví Dụ Minh Họa
Giả sử chúng ta có một đồ thị đơn giản với các đỉnh và trọng số như sau:
- Điểm bắt đầu: A
- Điểm đích: F
- Các cạnh và trọng số: A-B (1), A-C (4), B-C (2), B-D (5), C-E (1), D-F (2), E-F (3)
Hàm heuristic ước lượng khoảng cách từ các điểm đến F:
- h(A) = 7, h(B) = 6, h(C) = 2, h(D) = 1, h(E) = 3, h(F) = 0
- Khởi Tạo:
- Đặt A vào danh sách mở với 𝑓(𝐴) = 7.
- Lặp Lại:
- Chọn A từ danh sách mở và di chuyển A sang danh sách đóng.
- Xem xét các nút kề B và C:
- 𝑓(𝐵) = 𝑔(𝐵) + ℎ(𝐵) = 1 + 6 = 7
- 𝑓(𝐶) = 𝑔(𝐶) + ℎ(𝐶) = 4 + 2 = 6
- Đặt B và C vào danh sách mở.
- Tiếp Tục Lặp Lại:
- Chọn C (vì 𝑓(𝐶) = 6 nhỏ nhất).
- Xem xét các nút kề E:
- 𝑓(𝐸) = 𝑔(𝐸) + ℎ(𝐸) = 5 + 3 = 8
- Đặt E vào danh sách mở.
- Lặp Lại Cho Đến Khi Tìm Thấy F:
- Cuối cùng, chọn F khi nó xuất hiện trong danh sách mở với chi phí nhỏ nhất.
5. Ưu Điểm và Nhược Điểm
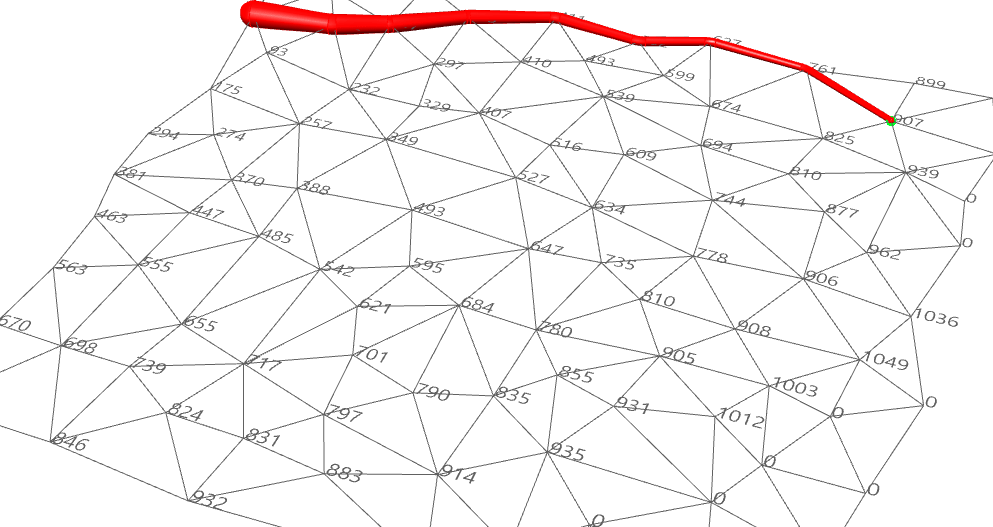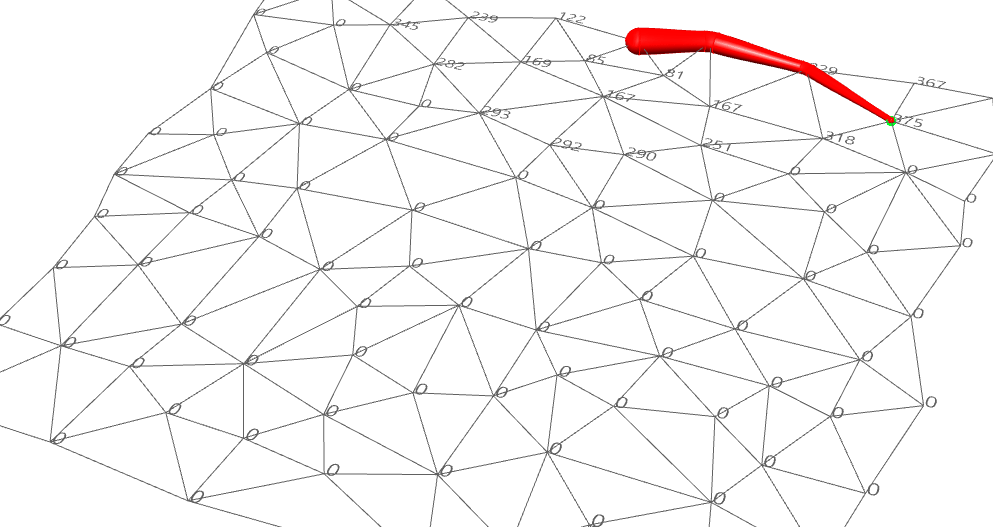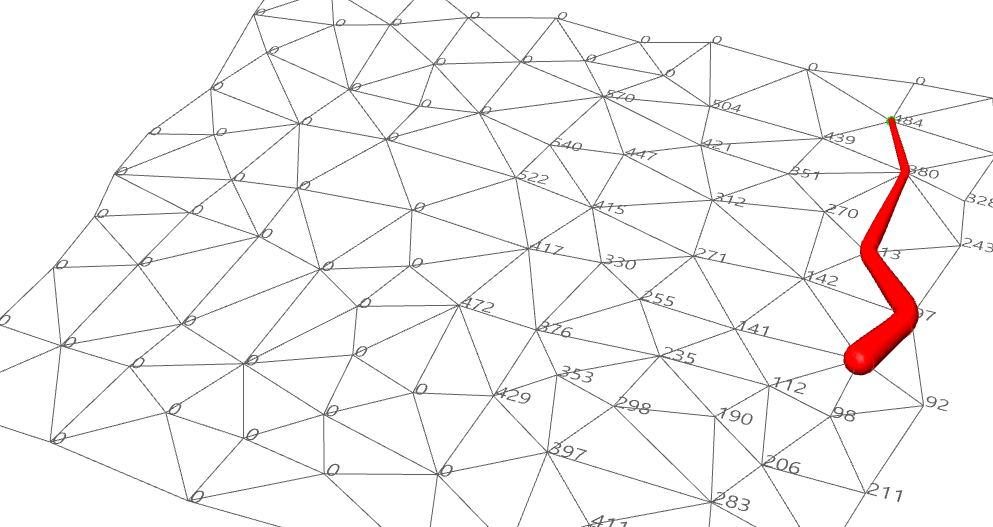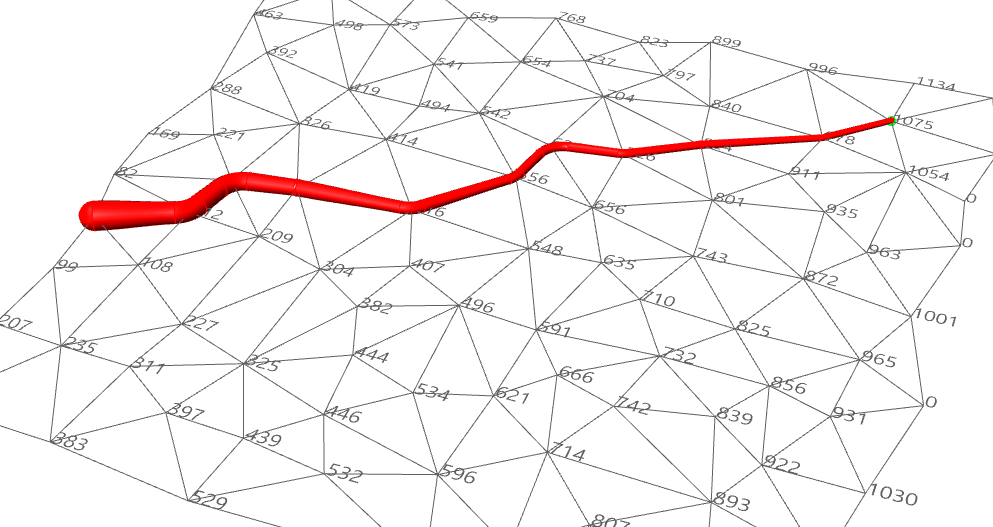
Ưu Điểm:
- Hiệu Quả: A* thường rất nhanh và tìm ra đường đi ngắn nhất nhờ sử dụng thông tin heuristic.
- Đảm Bảo Tối Ưu: A* đảm bảo tìm được đường đi ngắn nhất nếu hàm heuristic ℎ(𝑛)h(n) không vượt quá chi phí thực tế từ điểm hiện tại đến điểm đích.
Nhược Điểm:
- Tiêu Tốn Bộ Nhớ: A* có thể tiêu tốn nhiều bộ nhớ vì lưu trữ nhiều nút trong danh sách mở.
- Phụ Thuộc Heuristic: Hiệu quả của A* phụ thuộc vào chất lượng của hàm heuristic. Nếu heuristic không tốt, thuật toán có thể trở nên kém hiệu quả.
6. Ứng Dụng Thực Tiễn
- Định Tuyến GPS: A* được sử dụng để tìm đường đi ngắn nhất trong hệ thống định vị GPS.
- Lập Trình Game: Thuật toán này thường được sử dụng trong lập trình AI cho game để điều khiển các nhân vật tìm đường.
- Robot: A* giúp robot tìm đường đi tối ưu trong môi trường thực tế.
Thuật toán A* là một công cụ mạnh mẽ và hiệu quả để tìm đường ngắn nhất trong đồ thị, được ứng dụng rộng rãi trong nhiều lĩnh vực của cuộc sống và công nghệ.



