Thuật toán Knuth-Morris-Pratt (KMP) là một trong những thuật toán quan trọng trong lĩnh vực khoa học máy tính và xử lý chuỗi. Được phát triển bởi Donald Knuth, Vaughan Pratt và James H. Morris, thuật toán KMP giải quyết hiệu quả vấn đề đối sánh chuỗi, đặc biệt là khi chúng ta cần tìm kiếm một chuỗi con trong một chuỗi lớn.
1. Đối Sánh Chuỗi Là Gì?
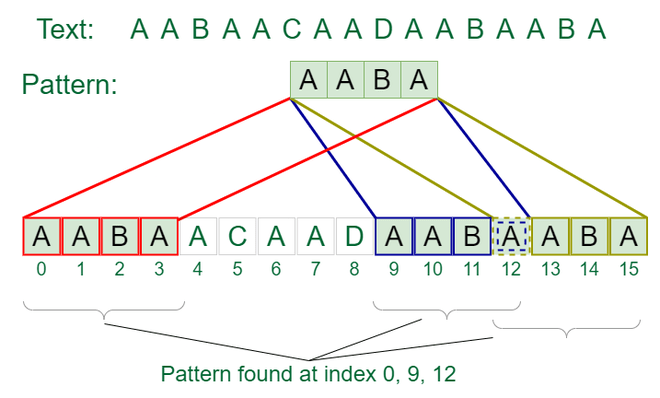
Trước khi bắt đầu với thuật toán KMP, chúng ta cần hiểu rõ về đối sánh chuỗi là gì. Đối sánh chuỗi là quá trình tìm kiếm một chuỗi con trong một chuỗi lớn. Ví dụ, nếu chúng ta có chuỗi “ABCAB” và muốn tìm kiếm chuỗi con “CA”, thuật toán đối sánh chuỗi sẽ giúp chúng ta xác định vị trí xuất hiện của chuỗi con trong chuỗi lớn.
2. Thuật Toán KMP là Gì?
2.1 Ý Tưởng Cơ Bản
Thuật toán KMP sử dụng một bảng gia tăng (lps – longest proper prefix which is also suffix) để giảm số lần so sánh cần thiết khi tìm kiếm chuỗi con. Bảng lps này được xây dựng trước khi thực hiện quá trình đối sánh.
2.2 Bước Xây Dựng Bảng LPS
Cho một chuỗi con P, bảng lps cho biết độ dài của chuỗi con lớn nhất, bắt đầu từ đầu chuỗi, mà là tiền tố và đồng thời là hậu tố của chuỗi con. Bảng lps được xây dựng một cách thông minh để giảm thời gian tìm kiếm.
P: A B A B A C
lps: 0 0 1 2 3 0
2.3 Bước Tìm Kiếm
Khi thực hiện quá trình tìm kiếm, ta so sánh các ký tự từ trái sang phải. Nếu có sự không khớp, ta sử dụng bảng lps để dịch chuyển chuỗi con một cách thông minh, giảm số lần so sánh không cần thiết.
3. Mã Nguồn Triển Khai KMP
Dưới đây là một ví dụ về mã nguồn Python triển khai thuật toán KMP:
def build_lps(pattern):
m = len(pattern)
lps = [0] * m
j = 0
for i in range(1, m):
while j > 0 and pattern[i] != pattern[j]:
j = lps[j - 1]
if pattern[i] == pattern[j]:
j += 1
lps[i] = j
return lps
def kmp_search(text, pattern):
n = len(text)
m = len(pattern)
lps = build_lps(pattern)
j = 0
for i in range(n):
while j > 0 and text[i] != pattern[j]:
j = lps[j - 1]
if text[i] == pattern[j]:
j += 1
if j == m:
print(f"Found pattern at index {i - j + 1}")
j = lps[j - 1]
# Example Usage
text = "ABABABABCA"
pattern = "ABABC"
kmp_search(text, pattern)
4. Ưu Điểm của KMP
- Hiệu Quả: KMP giảm độ phức tạp của quá trình đối sánh chuỗi, đặc biệt là trong trường hợp của các chuỗi lớn.
- Khả Năng Ứng Dụng Rộng Rãi: Thuật toán này có thể áp dụng trong nhiều lĩnh vực như xử lý văn bản, tìm kiếm chuỗi trong cơ sở dữ liệu, và nhiều ứng dụng khác.
5. Kết Luận
Trong bài viết này, chúng ta đã tìm hiểu về thuật toán KMP và cách triển khai nó thông qua mã nguồn Python. Hiểu rõ về cách KMP hoạt động có thể giúp tối ưu hóa quá trình tìm kiếm chuỗi, đồng thời nâng cao hiệu suất của các ứng dụng xử lý chuỗi.



