Selection Sort: Hiểu về thuật toán sắp xếp chọn

Sắp xếp là một trong những vấn đề cơ bản và quan trọng trong khoa học máy tính và lập trình. Nói một cách đơn giản, sắp xếp là quá trình sắp xếp các phần tử trong một danh sách theo một thứ tự nhất định. Một trong những thuật toán phổ biến được sử dụng để giải quyết vấn đề này là Selection Sort.

1. Khái quát

Selection Sort là một thuật toán đơn giản sử dụng để sắp xếp một danh sách các phần tử. Ý tưởng cơ bản của thuật toán là chọn phần tử nhỏ nhất từ danh sách và đưa nó vào vị trí đầu tiên. Tiếp theo, chọn phần tử nhỏ nhất tiếp theo và đưa nó vào vị trí thứ hai. Quá trình này được lặp lại cho tới khi danh sách được sắp xếp hoàn chỉnh.

2. Cách hoạt động

Đầu tiên ta giả sử cho ví dụ: arr[] = [64, 25, 12, 22, 11]

Bước 1:

Đối với vị trí đầu tiên trong mảng được sắp xếp, toàn bộ mảng được duyệt tuần tự từ index 0 đến 4. Vị trí đầu tiên hiện đang lưu trữ 64 , sau khi duyệt toàn bộ mảng, rõ ràng 11 là giá trị thấp nhất.
Do đó, thay thế 64 bằng 11. Sau một lần lặp 11 , giá trị nhỏ nhất trong mảng, có xu hướng xuất hiện ở vị trí đầu tiên của danh sách được sắp xếp.

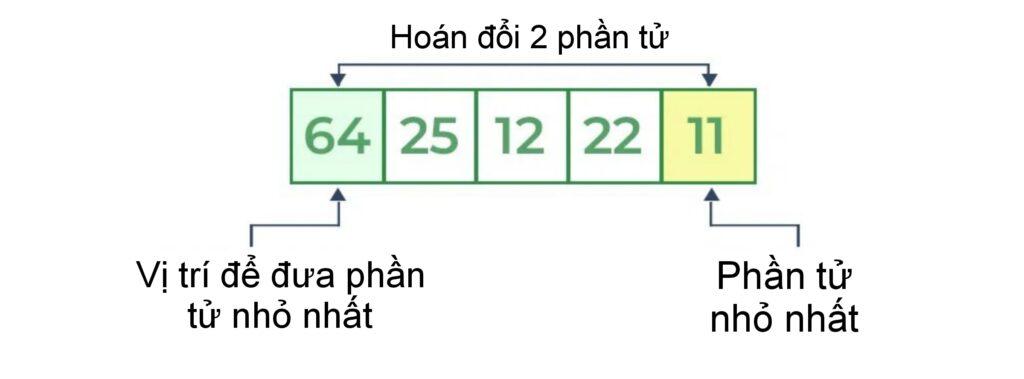
Bước 2:

Đối với vị trí thứ hai, vị trí mà có số 25, lại duyệt phần còn lại của mảng theo cách tuần tự.
Sau khi duyệt qua, chúng tôi thấy rằng 12 là giá trị thấp thứ hai trong mảng và nó sẽ xuất hiện ở vị trí thứ hai trong mảng, do đó hoán đổi các giá trị này.

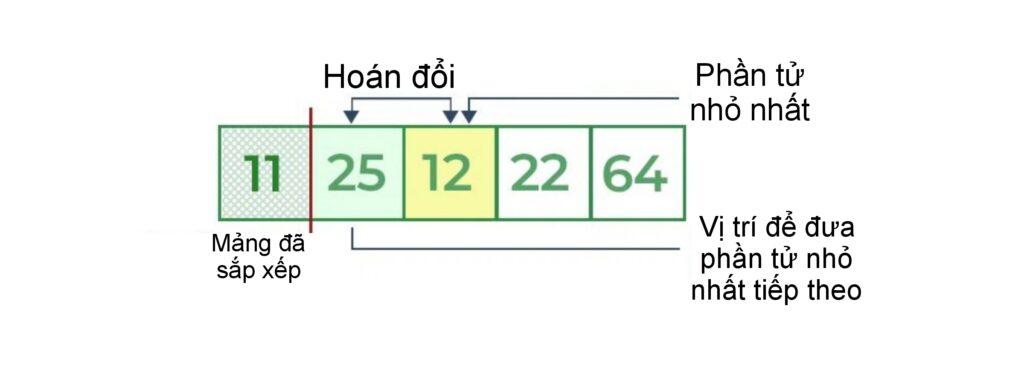
Bước 3:

Bây giờ, đối với vị trí thứ ba, trong đó 25 lại xuất hiện, duyệt qua phần còn lại của mảng và tìm giá trị nhỏ thứ ba có trong mảng.
Trong khi duyệt ngang, 22 trở thành giá trị nhỏ thứ ba và nó sẽ xuất hiện ở vị trí thứ ba trong mảng, do đó hoán đổi 22 với phần tử có mặt ở vị trí thứ ba.

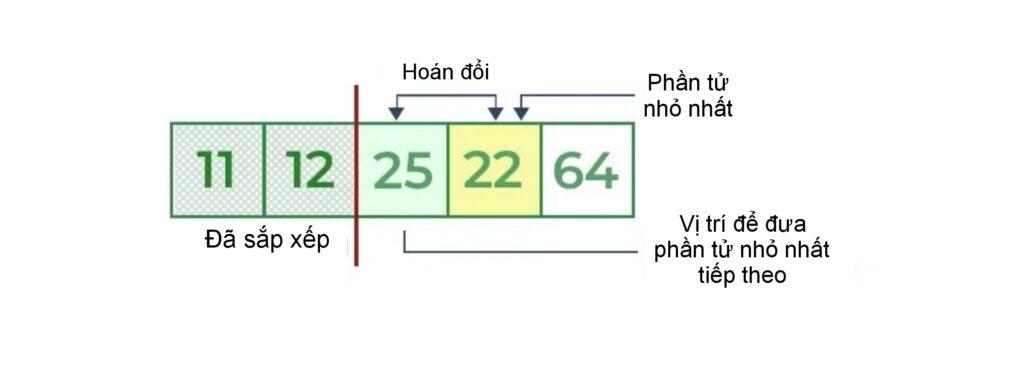
Bước 4:

Tương tự, đối với vị trí thứ tư, duyệt phần còn lại của mảng và tìm phần tử nhỏ thứ tư trong mảng
Vì 25 là giá trị thấp thứ 4 nên nó sẽ ở vị trí thứ 4.

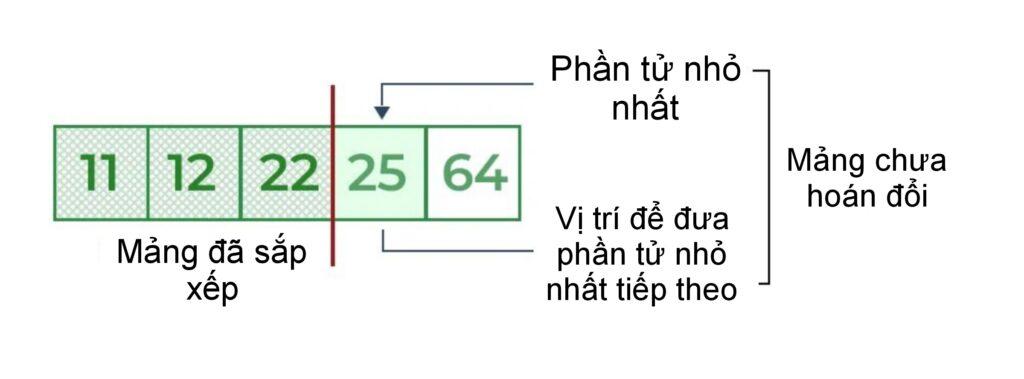
Bước 5:

Cuối cùng, giá trị lớn nhất có trong mảng sẽ tự động được đặt ở vị trí cuối cùng trong mảng
Mảng kết quả là mảng được sắp xếp.

3: Code thuật toán

function selectionSort(arr) {
    const n = arr.length;
    for (let i = 0; i < n - 1; i++) {
        let minIndex = i;
        for (let j = i + 1; j < n; j++) {
            if (arr[j] < arr[minIndex]) {
                minIndex = j;
            }
        }
        if (minIndex !== i) {
            // Swap arr[i] và arr[minIndex]
            [arr[i], arr[minIndex]] = [arr[minIndex], arr[i]];
        }
    }
    return arr;
}

// Ví dụ sử dụng
const arr = [64, 25, 12, 22, 11];
console.log("Danh sách trước khi sắp xếp: ", arr);
console.log("Danh sách sau khi sắp xếp: ", selectionSort(arr));

4. Phân tích độ phức tạp của thuật toán sắp xếp chọn

Độ phức tạp về thời gian: Độ phức tạp về thời gian của Sắp xếp lựa chọn là O(N ² ) vì có hai vòng lặp lồng nhau:

Một vòng lặp để chọn từng phần tử của Mảng = O(N)
Một vòng lặp khác để so sánh phần tử đó với mọi phần tử mảng khác = O(N)
Do đó độ phức tạp tổng thể = O(N) * O(N) = O(N*N) = O(N ² )

Không gian phụ trợ: O(1) là bộ nhớ bổ sung duy nhất được sử dụng cho các biến tạm thời trong khi hoán đổi hai giá trị trong Array. Việc sắp xếp lựa chọn không bao giờ thực hiện nhiều hơn O(N) hoán đổi và có thể hữu ích khi việc ghi bộ nhớ tốn kém.

5. Ưu và nhược điểm

5.1 Ưu điểm

Dễ hiểu và cài đặt.
Có thể sử dụng khi số lượng phần tử nhỏ hoặc danh sách gần như đã được sắp xếp.

5.2 Nhược điểm

Độ phức tạp cao với các danh sách lớn.
Sắp xếp lựa chọn có độ phức tạp về thời gian là O(N ²) trong trường hợp xấu nhất và trung bình.
Không hoạt động tốt trên các tập dữ liệu lớn.
Không bảo toàn thứ tự tương đối của các mục có khóa bằng nhau nghĩa là nó không ổn định.

6. Kết luận

Selection Sort là một thuật toán sắp xếp đơn giản nhưng không hiệu quả với các danh sách lớn. Nó thích hợp cho các trường hợp nhỏ và khi danh sách gần như đã được sắp xếp. Để hiểu rõ hơn về cách hoạt động của thuật toán, việc hiểu mã giả và phân tích độ phức tạp là rất quan trọng.

7. Tài liệu

Bạn cũng có thể vào trang web này để đọc thêm nhiều hơn nữa nhé: https://www.geeksforgeeks.org/selection-sort/