Quick Sort: Hiểu về thuật toán QuickSort

Quick Sort là một thuật toán sắp xếp rất hiệu quả và phổ biến trong lĩnh vực khoa học máy tính. Thuật toán này thuộc loại sắp xếp nhanh (quick sort), được phát minh bởi nhà khoa học máy tính người Anh Tony Hoare vào năm 1959 và sau đó được phát triển vào năm 1961.

1. Cách hoạt động của thuật toán Quick Sort

Ta sẽ cho 1 ví dụ mảng: arr[] = [10, 80, 30, 90, 40]

1.1 Chọn phần tử chốt (pivot):

• Luôn chọn phần tử đầu tiên làm trục xoay
• Luôn chọn phần tử cuối cùng làm trục (được triển khai bên dưới)
• Chọn một phần tử ngẫu nhiên làm điểm xoay
• Chọn phần giữa làm trục.

2.2 Thuật toán phân vùng

So sánh 10 với trục và vì nó nhỏ hơn trục, hãy sắp xếp nó theo cách tích lũy.

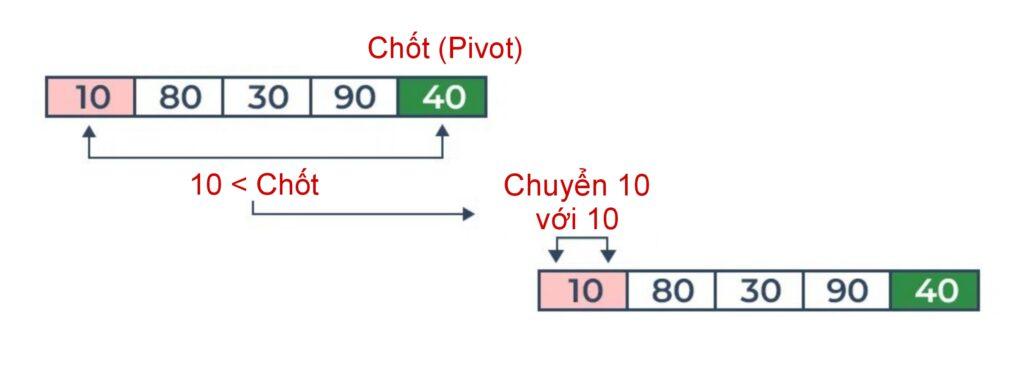
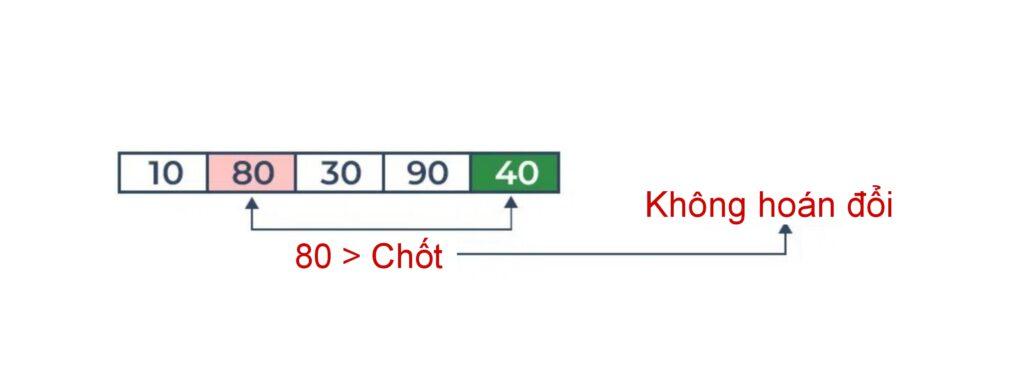
So sánh 80 với trục xoay. Nó lớn hơn trục.

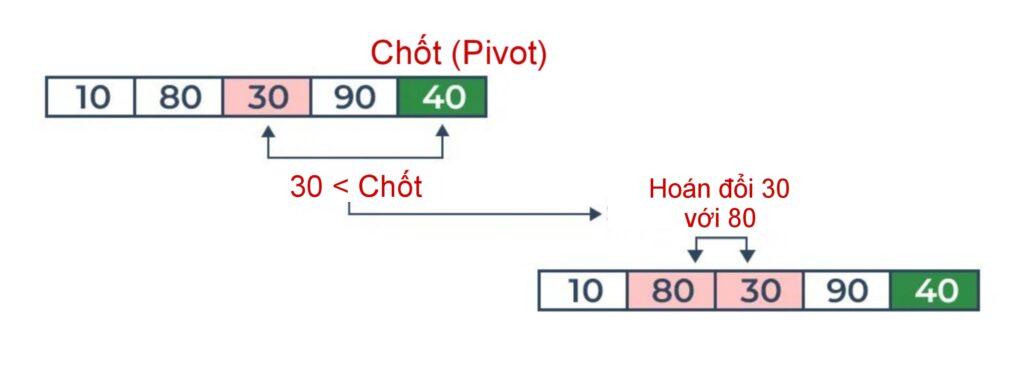
So sánh 30 với trục xoay. Nó nhỏ hơn trục nên hãy sắp xếp nó cho phù hợp.

So sánh 90 với trục xoay. Nó lớn hơn trục quay.

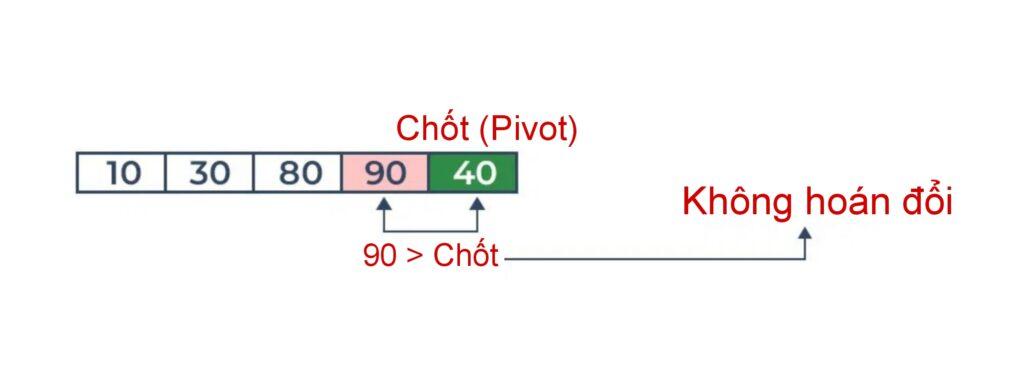
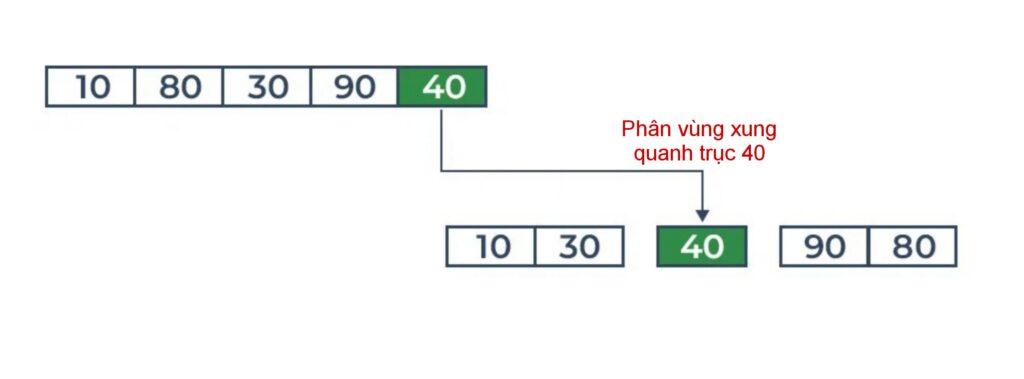
Sắp xếp trục xoay vào đúng vị trí của nó.

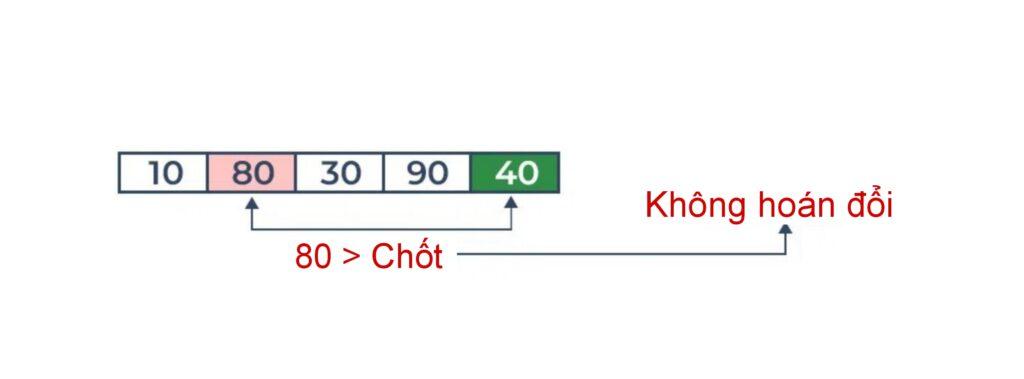
1.3 Minh hoạ Quick Sort

Khi quá trình phân vùng được thực hiện đệ quy, nó tiếp tục đặt trục xoay vào vị trí thực tế của nó trong mảng đã sắp xếp. Việc đặt các trục xoay liên tục vào vị trí thực tế của chúng sẽ làm cho mảng được sắp xếp.

Hãy theo dõi các hình ảnh bên dưới để hiểu cách triển khai đệ quy của thuật toán phân vùng giúp sắp xếp mảng như thế nào.

2. Code thuật toán Quick Sort

function quickSort(arr, low, high) {
    if (low < high) {
        /* pi là chỉ số chính của pivot sau khi được phân chia */
        let pi = partition(arr, low, high);

        quickSort(arr, low, pi - 1);  // Sắp xếp các phần tử trước pivot
        quickSort(arr, pi + 1, high); // Sắp xếp các phần tử sau pivot
    }
}

function partition(arr, low, high) {
    // Chọn phần tử chốt là phần tử cuối cùng của mảng
    let pivot = arr[high];  
    // Index của phần tử nhỏ hơn pivot
    let i = low - 1;

    for (let j = low; j <= high - 1; j++) {
        // Nếu phần tử hiện tại nhỏ hơn hoặc bằng pivot
        if (arr[j] <= pivot) {
            i++;    
            // Hoán đổi arr[i] và arr[j]
            let temp = arr[i];
            arr[i] = arr[j];
            arr[j] = temp;
        }
    }
    // Hoán đổi arr[i + 1] và arr[high])
    let temp = arr[i + 1];
    arr[i + 1] = arr[high];
    arr[high] = temp;

    return i + 1;
}

// Ví dụ về việc sử dụng Quick Sort
let arr = [10, 7, 8, 9, 1, 5];
let n = arr.length;
quickSort(arr, 0, n - 1);
console.log("Mảng đã sắp xếp: ", arr);

3. Phân tích độ phức tạp

Độ phức tạp về thời gian:

• Trường hợp Tốt nhất : Ω (N log (N))
  Trường hợp tốt nhất cho sắp xếp nhanh xảy ra khi trục được chọn ở mỗi bước chia mảng thành hai nửa gần bằng nhau.
  Trong trường hợp này, thuật toán sẽ tạo các phân vùng cân bằng, dẫn đến việc sắp xếp hiệu quả.
• Trường hợp trung bình: θ ( N log (N)) Hiệu suất trường hợp trung bình của Quicksort thường rất tốt trong thực tế, khiến nó trở thành một trong những Thuật toán sắp xếp nhanh nhất.
• Trường hợp xấu nhất: O(N2) Trường hợp xấu nhất đối với Quicksort xảy ra khi trục xoay ở mỗi bước luôn dẫn đến các phân vùng rất mất cân bằng. Khi mảng đã được sắp xếp và trục luôn được chọn là phần tử nhỏ nhất hoặc lớn nhất. Để giảm thiểu Trường hợp xấu nhất, nhiều kỹ thuật khác nhau được sử dụng như chọn một trục xoay tốt (ví dụ: trung vị của ba) và sử dụng thuật toán ngẫu nhiên hóa (Randomized Quicksort) để xáo trộn phần tử trước khi sắp xếp.
• Không gian phụ trợ: O(1), nếu chúng ta không xem xét không gian ngăn xếp đệ quy. Nếu chúng ta xem xét không gian ngăn xếp đệ quy thì trong trường hợp xấu nhất, quicksort có thể tạo ra  O ( N ).

4. Ưu và nhược điểm

4.1 Ưu điểm

• Đó là một thuật toán chia để trị giúp giải quyết vấn đề dễ dàng hơn.
• Nó hiệu quả trên các tập dữ liệu lớn.
• Nó có chi phí hoạt động thấp vì chỉ cần một lượng nhỏ bộ nhớ để hoạt động.

4.2 Nhược điểm

• Nó có độ phức tạp về thời gian trong trường hợp xấu nhất là O(N ² ), xảy ra khi trục được chọn kém.
• Nó không phải là một lựa chọn tốt cho các tập dữ liệu nhỏ.
• Đây không phải là kiểu sắp xếp ổn định, nghĩa là nếu hai phần tử có cùng khóa, thứ tự tương đối của chúng sẽ không được giữ nguyên trong kết quả được sắp xếp trong trường hợp sắp xếp nhanh, vì ở đây chúng ta đang hoán đổi các phần tử theo vị trí của trục xoay (không xem xét ban đầu của chúng). các vị trí).

5. Ứng dụng thực tế của Quick Sort

• Quản lý cơ sở dữ liệu: Sắp xếp thông tin trong các hệ thống quản lý cơ sở dữ liệu như danh sách khách hàng, sản phẩm, đơn hàng, bài viết theo thứ tự thời gian, thứ tự chữ cái hoặc tiêu chí khác.
• Tối ưu hóa tìm kiếm: Cải thiện hiệu suất tìm kiếm trong các cơ sở dữ liệu và ứng dụng bằng cách sắp xếp dữ liệu theo thứ tự để tối ưu hóa thời gian truy cập.
• Xử lý và phân tích dữ liệu lớn: Sử dụng trong các hệ thống xử lý và phân tích dữ liệu lớn để sắp xếp và phân chia dữ liệu một cách hiệu quả.
• Ứng dụng web: Sắp xếp dữ liệu hiển thị trên giao diện người dùng của các ứng dụng web, bao gồm danh sách sản phẩm, bài viết, bình luận, vv.
• Hệ thống tìm kiếm: Tối ưu hóa các hệ thống tìm kiếm để truy vấn và trả về kết quả nhanh chóng từ các tập dữ liệu lớn.
• Xử lý văn bản và tài liệu: Sắp xếp và tìm kiếm trong các tập dữ liệu văn bản và tài liệu, như sách, báo cáo, văn bản kỹ thuật, và nhiều hơn nữa.

6. Tài liệu

Bạn cũng có thể truy cập vào tài liệu này để hiểu hơn về Quick Sort nhé: https://www.geeksforgeeks.org/quick-sort/