Quantum Computing – Sự vướng víu lượng tử và dịch chuyển tức thời là những hiện tượng hấp dẫn trong thế giới cơ học lượng tử. Chúng liên quan đến mối liên hệ bí ẩn giữa các hạt và khả năng truyền tải thông tin mà không cần chuyển động vật lý. Trong bài đăng trên blog này, chúng tôi sẽ khám phá hai khái niệm cơ bản này, cung cấp một ví dụ đơn giản về dịch chuyển tức thời lượng tử bằng Qiskit và giúp bạn hiểu cách thức vướng víu cho phép dịch chuyển tức thời thông tin lượng tử trong không gian.

Người kiến dịch chuyển tức thời bằng công nghệ lượng tử viễn tưởng
Sự vướng víu lượng tử – Kết nối các trạng thái lượng tử
Sự vướng víu lượng tử là một hiện tượng đặc biệt kết nối các trạng thái lượng tử của các hạt, bất kể khoảng cách của chúng với nhau. Khi các hạt trở nên vướng víu, việc đo một hạt sẽ ngay lập tức ảnh hưởng đến hạt kia, ngay cả khi chúng cách nhau nhiều năm ánh sáng. Hành vi kỳ quái này, được Einstein đặt ra là “tác dụng ma quái ở khoảng cách xa”, thách thức hiểu biết cổ điển của chúng ta về vật lý.
Bây giờ chúng ta sẽ thiết lập kết nối lượng tử bằng cách tạo ra một cặp qubit vướng víu. Đầu tiên, chúng ta cần kích hoạt một mạch gồm hai qubit.
import numpy as np
from qiskit import QuantumCircuit, QuantumRegister, ClassicalRegister, execute, BasicAer, IBMQ
from qiskit.visualization import plot_histogram, plot_bloch_multivector,plot_bloch_vector
from qiskit import *
import matplotlib.pyplot as plt
%matplotlib inline
from qiskit.visualization import plot_histogram
alice = QuantumRegister(1, name='Alice')
bob = QuantumRegister(1, name='Bob')
qc = QuantumCircuit(alice,bob)
qc.draw('mpl')
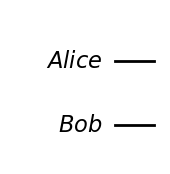
Sau đó, ta áp dụng cổng H và cổng CNOT để tạo thành một cặp vướng víu.
qc.h(alice[0])
qc.cx(alice[0],bob[0])
qc.draw('mpl')
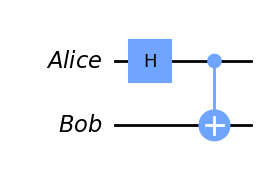
Đừng quên thêm các thanh ghi cổ điển để lưu trữ số đo của hai qubit này.
alice_classical_reg = ClassicalRegister(1,'Alice_class_reg')
bob_classical_reg = ClassicalRegister(1,'Bob_class_reg')
qc.add_register(alice_classical_reg)
qc.add_register(bob_classical_reg)
qc.draw('mpl')
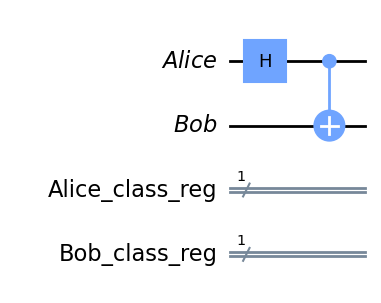
Bây giờ, chúng ta có thể đo giá trị của các qubit này
qc.measure(alice[0],alice_classical_reg)
qc.measure(bob[0],bob_classical_reg)
qc.draw('mpl')

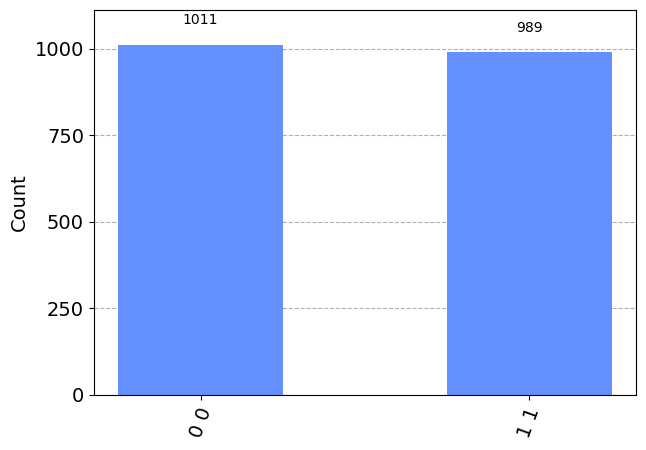
Do hiệu ứng vướng víu lượng tử, chúng ta có thể thấy hai qubit này kết thúc bằng ∣00> hoặc ∣11> với khả năng 50-50.
backend = BasicAer.get_backend('qasm_simulator')
res = execute(qc, backend,shots =2000).result()
plot_histogram( res.get_counts())
Dịch chuyển lượng tử
Dựa trên khái niệm vướng víu, chúng ta có dịch chuyển tức thời lượng tử. Dịch chuyển tức thời lượng tử là một quá trình cho phép chuyển trạng thái lượng tử từ vị trí này sang vị trí khác mà không cần qubit di chuyển qua không gian can thiệp. Hiện tượng này dựa trên logic kỳ lạ của cơ học lượng tử và có ý nghĩa mạnh mẽ đối với truyền thông lượng tử.
Hiểu về dịch chuyển lượng tử
Mục tiêu của dịch chuyển tức thời lượng tử là vận chuyển một trạng thái lượng tử chưa xác định một cách đáng tin cậy từ nơi này sang nơi khác. Nó sử dụng một cặp qubit vướng víu và giao tiếp cổ điển để đạt được thành tích này.
Các bước cơ bản liên quan là:
- Một cặp qubit vướng víu (1 và 2) được tạo ra và qubit 2 được trao cho người nhận Bob.
- Người gửi Alice có một số qubit không xác định (qubit 0) mà cô ấy muốn dịch chuyển đến Bob.
- Alice thực hiện phép đo chung trên qubit 0 và qubit 1, làm giảm trạng thái của chúng dựa trên các quy tắc của cơ học lượng tử.
- Alice gửi kết quả đo cổ điển cho Bob thông qua kênh liên lạc thông thường.
- Tùy thuộc vào tin nhắn từ Alice, Bob thực hiện các thao tác cổng thích hợp trên qubit 2 để tái tạo lại trạng thái của qubit 3.
Thì đấy! Trạng thái lượng tử chưa biết đã được dịch chuyển từ Alice sang Bob.
Mô phỏng dịch chuyển tức thời lượng tử với PennyLane
BƯỚC 0: ĐẦU TIÊN CHÚNG TA CẦN KHỞI TẠO HỆ THỐNG VỚI 3 QUBIT VÀ 2 THANH GHI CỔ ĐIỂN
target_info = QuantumRegister(1, name='target_info')
alice = QuantumRegister(1, name='Alice')
bob = QuantumRegister(1, name='Bob')
qc = QuantumCircuit(target_info,alice,bob)
alice_classical_reg = ClassicalRegister(1,'Alice_class_reg')
bob_classical_reg = ClassicalRegister(1,'Bob_class_reg')
qc.add_register(alice_classical_reg)
qc.add_register(bob_classical_reg)
qc.draw('mpl')
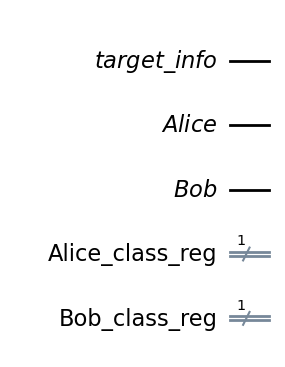
BƯỚC 1: SAU ĐÓ, CHÚNG TA TẠO RA MỘT CẶP QUBIT VƯỚNG VÍU.
Một cái do Alice giữ, một cái khác do Bob giữ
qc.h(alice[0])
qc.cx(alice[0],bob[0])
qc.draw('mpl')

BƯỚC 2: SAU ĐÓ, Ở PHÍA NGƯỜI GỬI, CHÚNG TA CHUẨN BỊ TRẠNG THÁI LƯỢNG TỬ MUỐN GỬI CHO BOB.
Ví dụ: ở đây chúng tôi có trạng thái để gửi
plot_bloch_vector([1, np.pi/4, -np.pi/2], coord_type='spherical')

qc.barrier()
qc.rx(np.pi/4,0)
qc.draw('mpl')
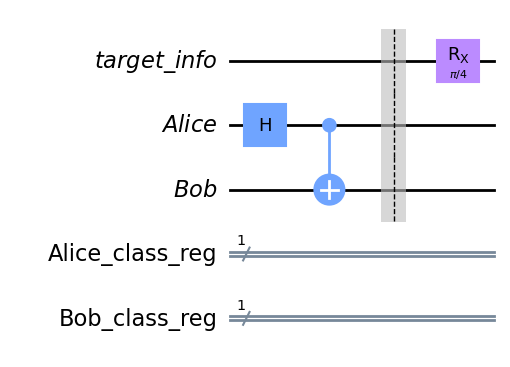
BƯỚC 3: TIẾP THEO, ALICE ÁP DỤNG TRẠNG THÁI LƯỢNG TỬ MỤC TIÊU CHO QUBIT CỦA MÌNH
qc.barrier()
qc.cx(target_info[0],alice[0])
qc.h(target_info[0])
qc.draw('mpl')
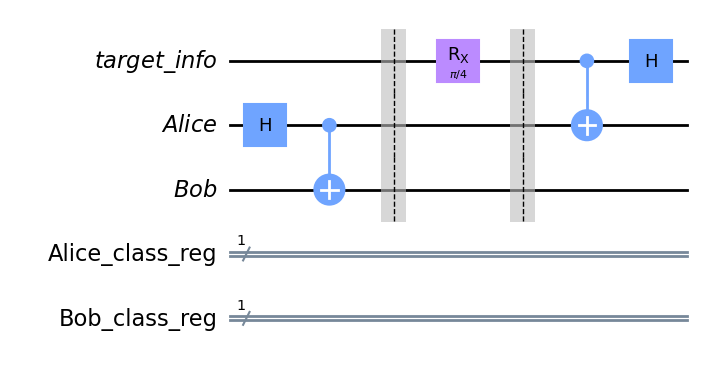
BƯỚC 4: ALICE ĐO TRẠNG THÁI CỦA QUBIT, LƯU TRỮ KẾT QUẢ DƯỚI DẠNG BIT CỔ ĐIỂN VÀ GỬI CHO BOB
qc.barrier()
qc.measure(target_info[0],alice_classical_reg)
qc.measure(alice[0],bob_classical_reg)
qc.draw('mpl')

BƯỚC 5: BOB GIẢI MÃ DỰA TRÊN SỐ BIT ANH ẤY NHẬN ĐƯỢC
qc.z(bob[0]).c_if(alice_classical_reg, 1) #if alice_classical_reg is 1 apply Z gate
qc.x(bob[0]).c_if(bob_classical_reg, 1) #if bob_classical_reg is 1 apply x gate
qc.draw('mpl')
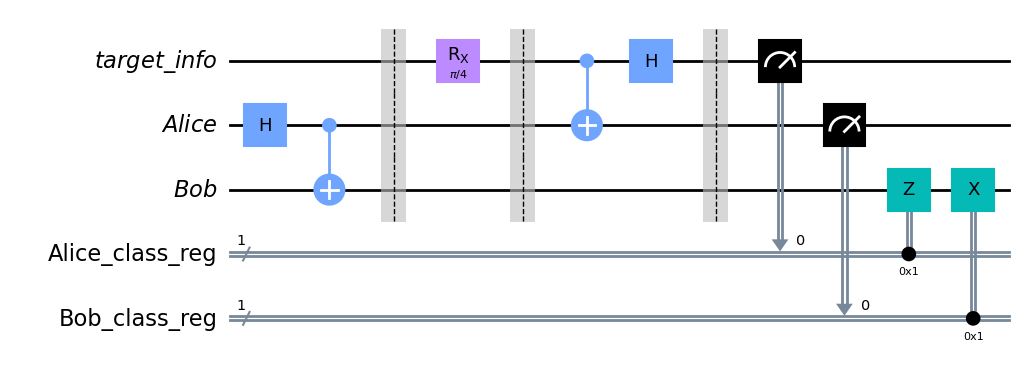
backend = BasicAer.get_backend('statevector_simulator')
out_vector = execute(qc, backend).result().get_statevector()
plot_bloch_multivector(out_vector)

Sau đó, trạng thái được gửi thành công tới Bob