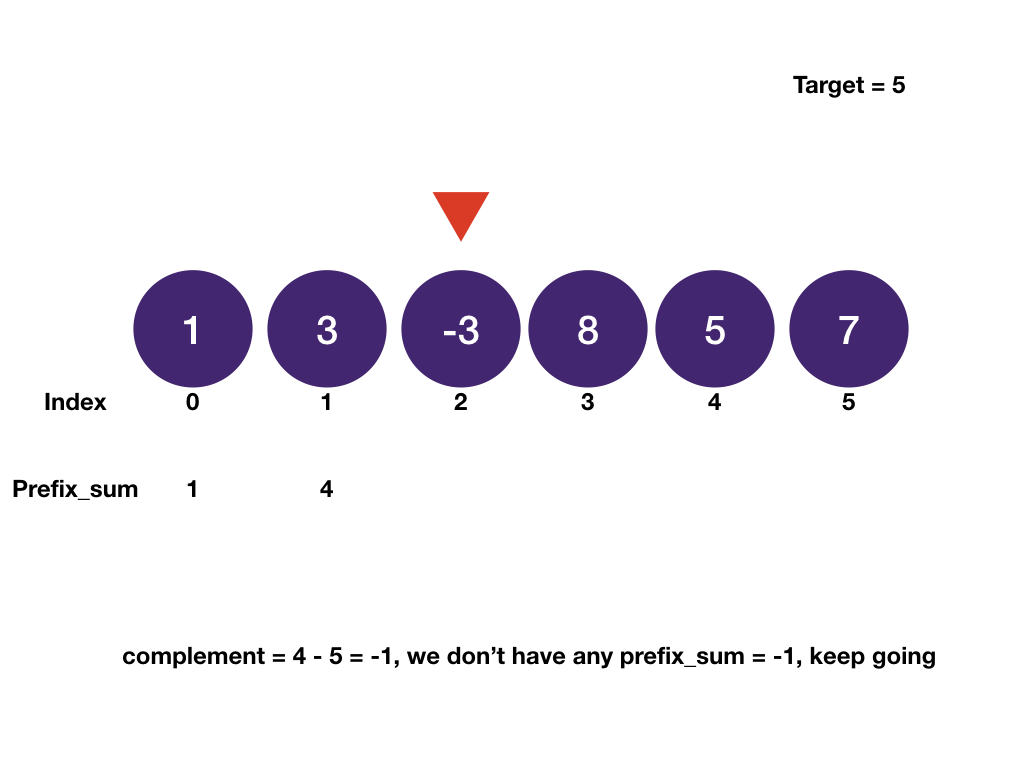
Prefix sum – một số bài toán ứng dụng

Prefix sum là một tổng giá trị của một dãy bắt đầu từ phần tử đầu tiên

Bài 1: QBSEQ – Dãy con dài nhất có tổng chia hết cho K

• Đề bài:
  • Cho một dãy gồm nnn (n≤100000) số nguyên dương A₁,A₂,…,A_n và một số nguyên dương k (k≤5000). Hãy tìm dãy con liên tiếp gồm nhiều phần tử nhất của dãy đã cho sao cho tổng các phần tử của dãy con này chia hết cho k.
  • INPUT
    • Dòng đầu tiên chứa hai số n,kn, kn,k cách nhau bởi ít nhất 1 dấu cách.
    • Dòng thứ hai chứa các số A₁,A₂,…,A_n được ghi theo đúng thứ tự cách nhau bởi ít nhất một dấu cách hoặc xuống dòng.
  • OUTPUT
    • Gồm một dòng duy nhất ghi số lượng phần tử của dãy con dài nhất thỏa mãn điều kiện.

• Hướng giải quyết:
  • Tạo 1 prefix sum sum với sum[i] = tổng các phần từ của mảng a từ 1 đến i sau khi lấy phần dư khi chia cho k
  • Nhận thấy tổng của 1 đoạn từ i đến j = sum[j] – sum[i-1] và số dư của 1 đoạn từ i đến j khi chia cho k = (sum[j] – sum[i-1] + k) %k
  • 1 đoạn từ i đến j chia hết cho k khi (sum[j] – sum[i-1] + k) %k = 0 hay nói cách khác sum[i] = sum[j].
  • Vậy nhiệm vụ của mình là tìm 1 khoảng i đến j dài nhất sao cho sum[i] = sum[j]. Cách giải quyết mình sẽ dùng một mảng để lưu lại vị trí đầu tiên xuất hiện của 1 số dư khi chia cho k trong mảng sum để cập nhật kết quả.
  • Trong lúc duyệt prefix sum, chúng ta không cần lưu giá trị lại nên chỉ cần dùng 1 biến để lưu lại giá trị prefix sum hiện tại.
    
• Code:

#include <bits/stdc++.h>
using namespace std;

int longestSubarrayDivisibleByK(vector<int> &arr, int k) {
    unordered_map<int, int> modIndex; // Lưu vị trí đầu tiên xuất hiện của mỗi mod k
    modIndex[0] = -1; // Khởi tạo dư 0 tại vị trí -1 để xử lý tổng từ đầu dãy
    int prefixSum = 0, maxLen = 0;

    for (int i = 0; i < arr.size(); i++) {
        prefixSum += arr[i];
        int mod = ((prefixSum % k) + k) % k; // Đảm bảo mod luôn dương

        if (modIndex.find(mod) != modIndex.end()) {
            maxLen = max(maxLen, i - modIndex[mod]); // Độ dài dãy con
        } else {
            modIndex[mod] = i; // Lưu vị trí đầu tiên xuất hiện của mod
        }
    }

    return maxLen;
}

int main() {
    int n, k;
    cin >> n >> k;
    vector<int> arr(n);
    for (int i = 0; i < n; i++) {
        cin >> arr[i];
    }

    cout << longestSubarrayDivisibleByK(arr, k) << endl;
    return 0;
}

Bài 2: Khối lập phương (CUBICS.*)

• Đề bài:
  • Jimmy có một bộ khối lập phương xếp thành n tháp với chiều cao khác nhau. Một dãy liên tục các tháp được coi là hài hòa nếu chúng có độ cao trung bình bằng k.
  • Yêu cầu:
    • Tìm dãy tháp dài nhất có trung bình bằng k.
    • Nếu có nhiều dãy có cùng độ dài, lấy dãy xuất hiện trước.
    • Nếu không có dãy nào thỏa mãn, xuất ra 0.
• Hướng giải quyết:
  • Biến đổi dãy số
    • Thay mỗi phần tử a[i] thành a'[i] = a[i] – k.
    • Bài toán trở thành: tìm dãy con có tổng bằng 0 dài nhất.
  • Dùng prefix sum + hashmap để tối ưu
    • Duyệt qua dãy, tính tổng cộng dồn (prefix sum).
    • Nếu gặp lại một tổng trước đó, ta có một dãy con có tổng bằng 0.
    • Lưu tổng vào hashmap để tìm nhanh.
• Code:

#include <bits/stdc++.h>
using namespace std;

pair<int, int> findLongestZeroSumSubarray(vector<int>& a, int n, int k) {
    unordered_map<long long, int> prefixMap;
    long long sum = 0;
    int maxLen = 0, startIdx = -1;

    prefixMap[0] = -1; // Xử lý trường hợp dãy con bắt đầu từ index 0

    for (int i = 0; i < n; i++) {
        sum += (a[i] - k); // Biến đổi phần tử

        if (prefixMap.find(sum) != prefixMap.end()) {
            int length = i - prefixMap[sum];
            if (length > maxLen) {
                maxLen = length;
                startIdx = prefixMap[sum] + 1; // Vị trí bắt đầu dãy con
            }
        } else {
            prefixMap[sum] = i; // Lưu vị trí tổng này đầu tiên
        }
    }

    return (maxLen == 0) ? make_pair(0, 0) : make_pair(maxLen, startIdx + 1);
}

int main() {
    ifstream fin("CUBICS.INP");
    ofstream fout("CUBICS.OUT");

    int n, k;
    fin >> n >> k;
    vector<int> a(n);
    
    for (int i = 0; i < n; i++) fin >> a[i];

    auto result = findLongestZeroSumSubarray(a, n, k);
    fout << result.first << " " << result.second << endl;

    return 0;
}