Trong lĩnh vực công nghệ thông tin, kĩ thuật thiết kế giải thuật phân hoạch, hay còn được gọi là chia để trị, là một phương pháp quan trọng trong việc giải quyết các bài toán phức tạp. Trong bài viết này, chúng ta sẽ tìm hiểu về giải thuật partition, một kỹ thuật phân hoạch thông qua việc chia nhỏ bài toán ban đầu thành các bài toán con nhỏ hơn.
Trước khi khám phá về giải thuật partition, chúng ta hãy nhìn lại giải thuật vét cạn (brute force). Giải thuật vét cạn thường được sử dụng khi không có phương pháp tối ưu nào khác và yêu cầu kiểm tra tất cả các khả năng có thể. Tuy nhiên, đây thường là một phương pháp chậm chạp và không hiệu quả với các bài toán lớn.
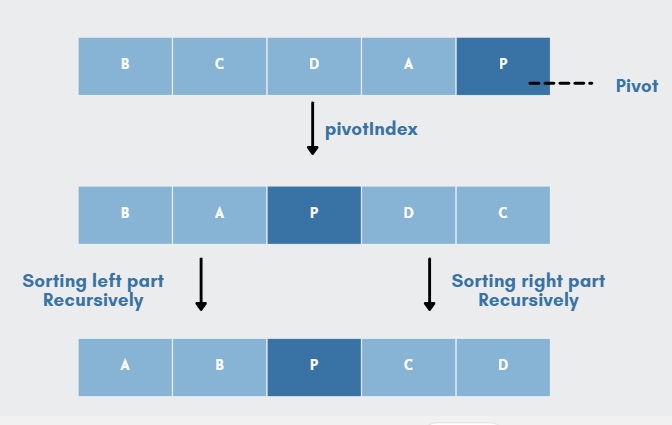
Partition – chia để trị
Giải thuật partition dựa trên nguyên lý chia để trị, trong đó bài toán ban đầu sẽ được chia thành các bài toán con nhỏ hơn. Quá trình này được lặp đi lặp lại cho đến khi các bài toán con đạt được kích thước nhỏ và dễ giải quyết. Sau đó, kết quả từ các bài toán con sẽ được kết hợp lại để giải quyết bài toán ban đầu.
Các bước trong giải thuật
- Chia để trị: Bước này tách bài toán ban đầu thành các bài toán con nhỏ hơn. Việc chia này có thể được thực hiện theo cách đệ quy hoặc theo cách lặp. Mục tiêu là để giảm kích thước của bài toán ban đầu.
- Giải quyết các bài toán con: Sau khi chia bài toán ban đầu thành các bài toán con nhỏ hơn, ta sẽ giải quyết từng bài toán con này một cách độc lập. Đây là giai đoạn quan trọng để đạt được kết quả cho từng bài toán con.
- Kết hợp kết quả: Kết quả từ các bài toán con sẽ được kết hợp lại để đưa ra kết quả cho bài toán ban đầu. Quá trình này tùy thuộc vào bài toán cụ thể và có thể là việc trộn, tính toán hoặc tổng hợp các kết quả con.
Ví dụ
Để minh họa giải thuật partition, chúng ta hãy xem xét một ví dụ cụ thể: tìm phần tử lớn thứ k trong một mảng.
- Chia để trị: Ta chia mảng thành các mảng con nhỏ hơn, ví dụ: nửa đầu và nửa sau của mảng.
- Giải quyết các bài toán con: Đối với từng mảng con, ta áp dụng giải thuật tìm phần tử lớn thứ k trên mảng con đó.
- Kết hợp kết quả: So sánh kết quả từ các mảng con và chọn phần tử lớn thứ k.
Ứng dụng của partition
Giải thuật partition được sử dụng rộng rãi trong nhiều lĩnh vực khác nhau trong công nghệ thông tin, bao gồm:
- Sắp xếp mảng: QuickSort là một ví dụ nổi tiếng về giải thuật partition trong việc sắp xếp mảng.
- Tìm kiếm nhị phân: Giải thuật Binary Search cũng sử dụng kỹ thuật partition để chia mảng và tìm kiếm phần tử.
Kết luận
Giải thuật partition là một kỹ thuật quan trọng trong thiết kế giải thuật phân hoạch (chia để trị) trong lĩnh vực công nghệ thông tin. Bằng cách chia bài toán ban đầu thành các bài toán con nhỏ hơn, giải thuật partition giúp chúng ta giải quyết các bài toán phức tạp một cách hiệu quả. Qua ví dụ về tìm phần tử lớn thứ k, chúng ta có thể thấy sự ứng dụng linh hoạt và rộng rãi của giải thuật partition trong các bài toán thực tế.



