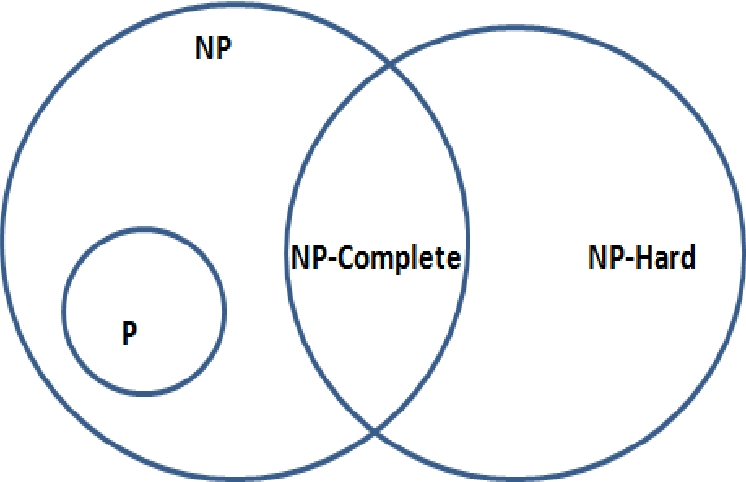
P vs. NP và vấn đề bảo mật
Vậy bài toán thiên niên kỷ P vs. NP có liên quan gì đến bảo mật. Mối liên quan ở đây là cực kỳ mật thiết.
Mọi vấn đề bảo mật hiện nay đều liên quan đến mã hoá. Và các hệ mã hoá hiện này đều được xây dựng dựa trên niềm tin rằng P ≠ NP. Niềm tin này cũng giống như toàn bộ các kiến thức hình học đều dựa trên niềm tin vào tiên đề Euclid vậy. Thậm chí niềm tin vào tiên đề Euclid có phần mù quáng hơn do nó đã được chứng minh là không thể chứng minh được.

Trong khi P ≠ NP là một điều chưa được chứng minh, nhưng cũng chưa bị phủ nhận. Các bài toán NP hiện nay đều yêu cầu một thuật toán phức tạp để tìm ra lời giải, có những bài toán phải mất hàng tỉ năm mới tìm ra được lời giải.
Một ví dụ cụ thể chính là hệ mã hoá RSA. Mức độ bảo mật của hệ mã hoá này phụ thuộc vào độ khó của bài toán: phân tích một số nguyên thành các nhân tử. Đây là một bài toán NP do kết quả của nó rất dễ dàng để kiểm chứng (nhân các nhân tử lại với nhau), nhưng việc tìm ra các nhân tử đó không hề dễ dàng một chút nào.
Về mặt thực tiễn, hiện tại chưa có một thuật toán hiệu quả nào có thể phân tích mọi số nguyên thành nhân tử trong thời gian đa thức. Về mặt lý thuyết, một thuật toán như vậy chưa được chứng minh là có tồn tại hay không. Và niềm tin rằng nó không tồn tại chính là cơ sở để tin rằng, hệ mã hoá RSA vẫn an toàn.
Vào thời điểm hiện tại, mọi cố gắng để giải bài toán này cũng chưa có một kết quả khả quan. Một nỗ lực của nhóm các nhà khoa học vào năm 2009, nhằm phân tích thành nhân tử một số của 232 chữ số (số RSA-768) cũng mất tới hai năm dù đã sử dụng hàng trăm máy tính. Một số RSA-1024 được dự đoán sẽ mất hàng nghìn năm để phân tích. Nhiều hệ thống hiện này còn sử dụng RSA-2048 trong mã hoá, khiến nó gần như không thể bị phá vỡ với công nghệ hiện tại.
Không chỉ riêng RSA, hầu như mọi hệ mã hoá đều đang an toàn bởi “niềm tin” rằng P ≠ NP, tức là phải mất nhiều năm để giải mã, nếu dùng một khoá đủ mạnh. Thế nhưng nếu chứng minh được P = NP thì mọi thứ sẽ sụp đổ, nhưng thứ được tin là an toàn, sẽ không còn an toàn nữa.
Không chỉ có các hệ mã hóa mất an toàn, rất nhiều khía cạnh của công nghệ hiện đại cũng sụp đổ. Bitcoin, Etherium, blockchain, những công nghệ rất hot hiện nay cũng sẽ sụp đổ nếu P = NP.
Nếu P = NP thì mức độ an toàn sẽ kém đến mức nào?
Thật may mắn là dù chứng minh được P = NP thì mọi thứ cũng không đến nổi quá tệ. Như đã nói ở trên, “nhanh chóng” hay “thời gian đa thức” là những khái niệm phức tạp trong toán học. Nếu một nhà toán học nói rằng, hệ mã hoá RSA có thể được phá vỡ một cách nhanh chóng, thì nhiều khi trong thực tế, việc đó cũng không “nhanh” lắm.
Mọi thứ còn phụ thuộc vào thuật toán được dùng để giải các bài toán NP nữa. Nếu trong trường hợp, một thuật toán giải các bài toán NP-complete với thời gian O(n ^ 4) thì đó không phải là thời gian quá lớn. Điều này sẽ khiến các hệ mã hoá hiện tại, kể cả loại đối xứng hay loại public key, đều không còn an toàn nữa. Trong lúc này, chỉ còn các hệ mã hoá đã được chứng minh là an toàn như one-time pad hay phương thức xác thực kiểu Carter-Wegan, là còn có thể bảo vệ được chúng ta.
Khi đó, các hệ mã hoá cũ không còn an toàn nữa, nhân loại phải tiếp tục thiết kế các hệ mã hoá mới an toàn hơn. Sẽ mất một vài năm để chúng ta chuyển qua các hệ mã hoá mới. Thế nhưng ngay cả những hệ mã hoá mới này cũng chưa chắc đã an toàn, bởi mọi bài toán có thể nhanh chóng kiểm chứng được lời giải, thì có thể nhanh chóng tìm ra lời giải đó.
Nếu hôm nay có một hệ mã hoá phải mất nhiều hơn O(n ^ 4) thời gian để giải, thì trong lúc nhân loại chưa kịp chuyển qua hệ mã hoá mới, rất có thể một thuật toán tối ưu hơn đã được đưa ra. Trong trường hợp này, mọi thứ cần phải được thiết kế lại, chứ không riêng gì việc mã hoá. Đó thực sự là một thảm hoạ.
Thế nhưng, nếu may mắn hơn, thuật toán để giải các bài toán NP-complete phải mất O(n ^ 100) thời gian để giải, thì tương lai cũng không quá khó khăn. Vì luỹ thừa 100 là một số khá lớn, chúng ta có thể tạm thời tăng mức độ bảo mật lên bằng cách tăng độ lớn của các khoá. Vì vậy, dù đã được chứng minh là kém an toàn, nhưng trong tương lai gần, chúng ta vẫn được bảo vệ.
Thế nhưng, cũng không nên hy vọng quá, bởi nhân tài thế giới nhiều vô cùng. Biết đâu sau một hoặc hai năm, có một thiên tài nào đó tối ưu hoá thuật toán đó về thời gian O(n ^ 10) hay thậm chí O(n ^ 4) để giải các bài toán NP-complete. Vâng, dù không có tác động ngay lập tức, nhưng việc chứng minh P = NP cũng có những ảnh hưởng rất đáng sợ.
May mắn nhất đối với chúng ta, là trường hợp có người chứng minh được P = NP nhưng không hề tìm ra được thuật toán nào để giải các bài toán NP trong thực tế, hoặc ít nhất là nó đủ nhanh trong thực tế. Khi dó chúng ta sẽ ở trong một tình trạng tương đối hỗn loạn khi lý thuyết thì bảo “có” nhưng thực tế thì lại nó “không”.
Tất cả những điều trên sẽ không thể xảy ra trong tương lai gần, vì bài toán thiên niên kỷ đâu có dễ giải đến thế. Vì vậy, nếu bạn đang tự hỏi mình nên làm thế nào để bảo vệ mình nếu có ai đó chứng minh được P = NP. Câu trả lời là đừng bận tâm đến nó, trước mắt, chúng ta có nhiều mối quan tâm thực tế hơn, như tình trạng theo dõi người dùng, cracker tấn công hệ thống đánh cắp thông tin, thông tin cá nhân bị rao bán tràn lan trên chợ đen, v.v…



