
Nếu như bạn là một người mới bắt đầu bước chân vào lĩnh vực học máy (Machine learning) bạn có lẽ sẽ tiếp cận với những Tutorial trên mạng theo hướng đi ăn xổi ở thì. Bạn có thể làm được một vài điều khá là hay ho, khá là kì diệu đối với bạn ở thời điểm đó như nhận diện được đâu là một chú mèo trong bức ảnh, dự đoán được biến động của thị trường chứng khoán ngày mai là như thế nào, chuẩn đoán được một người có phải bị bệnh HIV hay không…
Tất nhiên những thứ đó giúp cho bạn có thứ cảm giác rất sung sướng khi làm được một điều gì đó với lĩnh vực mới này. Tuy nhiên khi bạn càng tìm hiểu sâu về nó thì bạn sẽ thấy có những vấn đề không thể có một Tutorial nào cho bạn cả, bản thân bạn phải tự giải quyết nó.
Đến lúc đó bạn sẽ lại phải vòng ngược lại và tự vấn bản thân rằng vì sao người ta lại sử dụng thuật toán này để giải quyết bài toán đó???. Và đây chính là lúc bạn tìm về với lý thuyết xác suất một trong những lý thuyết cơ sở để hình thành nên nhưng thuật toán của Machine Learning.
Tác giả: Trần Hữu Tuấn
Trong phần 2 của loạt bài viết “Nhập môn Machine Learning”, chúng ta sẽ tiếp tục khám phá một khía cạnh quan trọng trong lĩnh vực Machine Learning, đó là lí thuyết xác suất. Xác suất là một công cụ mạnh mẽ giúp chúng ta hiểu và mô hình hóa sự không chắc chắn trong dữ liệu. Trong bài viết này, chúng ta sẽ đi qua các khái niệm cơ bản về xác suất và các tính chất quan trọng của nó.
Giới thiệu
Xác suất là một lĩnh vực trong toán học và thống kê nghiên cứu về việc đo lường và mô tả khả năng xảy ra của một sự kiện. Trong Machine Learning, xác suất là một yếu tố quan trọng để phân tích dữ liệu và xây dựng các mô hình dự đoán.
Không gian xác suất
Không gian xác suất là tập hợp của tất cả các kết quả có thể xảy ra trong một thí nghiệm hoặc một sự kiện. Chúng ta sẽ khám phá các khái niệm như sự kiện, phép toán trên các sự kiện, và các quy tắc cơ bản trong không gian xác suất.
Về mặt toán học, người ta kí hiệu một không gian xác suất – probability space bao gồm 3 thành phần (Ω,F,P) như sau:
- Ω chính là tập các giá trị có thể xảy ra – possible outcome với sự kiện trong không gian xác suất. Người ta còn gọi nó là không gian mẫu
- F⊆2Ω – (cái này là lũy thừa cơ số 2 của Ω) là tập hợp các sự kiện có thể xảy ra trong không gian xác suất
- P là xác suất (hoặc phân phối xác suất) của sự kiện. P ánh xạ một sự kiện E∈F vào trong một giá trị thực p∈[0;1]. Ở đây chúng ta gọi p=P(E) là xác suất của sự kiện E
Ví dụ minh họa
Hãy xem xét một ví dụ minh họa để hiểu rõ hơn về không gian xác suất. Giả sử chúng ta tung một con xúc xắc sáu mặt. Không gian xác suất của thí nghiệm này sẽ chứa các kết quả từ 1 đến 6. Các kết quả này được gọi là các sự kiện đơn lẻ và chúng có khả năng xảy ra như nhau.

Các tính chất của xác suất
Giống như ví dụ ở phía trên, khi không gian mẫu – outcomes space là hữu hạn thì chúng ta thường lựa chọn không gian sự kiện F=2Ω={∅,{1,3,5},{2,4,6},Ω}. Cách tiếp cận này chưa hẳn đã tổng quát hóa cho mọi trường hợp tuy nhiên nó đủ dùng trong các bài toán thực tế, tất nhiên là với giả thiết không gian mẫu của chúng ta là hữu hạn. Khi không gian mẫu là vô hạn – infinite chúng ta phải hết sức cẩn thận trong việc lựa chọn không gian sự kiện F. Khi đã định nghĩa dược không gian sự kiện F thì hàm xác suất của chúng ta bắt buộc phải thỏa mãn các tính chất sau đây:
- Không âm – non-negativity – xác suất của mọi sự kiện là không âm, tức là với mọi x∈F, P(x)≥0
- Xác suất toàn cục – trivial event P(Ω)=1
- Tính cộng – additivity tức là với mọi x,y∈F nếu như x∩y=∅ thì ta có P(x∪y)=P(x)+P(y)
Biến ngẫu nhiên – Random Variables
Biến ngẫu nhiên là một biến mà giá trị của nó phụ thuộc vào kết quả của một quá trình ngẫu nhiên. Chúng ta sẽ khám phá cách biểu diễn biến ngẫu nhiên và tìm hiểu về các loại biến ngẫu nhiên, bao gồm biến rời rạc và biến liên tục.
Biến rời rạc và biến liên tục
Biến rời rạc là biến mà các giá trị có thể rời rạc và đếm được, trong khi biến liên tục là biến mà các giá trị có thể liên tục và đo được.
Ví dụ tung xúc sắc bên trên là một điển hình của biến ngẫu nhiên rời rạc và hàm xác suất của nó được định nghĩa như sau:
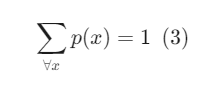
Còn biến ngẫu nhiên liên tục có thể định nghĩa là các biến ngẫu nhiên mà các giá trị của nó rơi vào một tập không biết trước. Trong Machine Learning người ta gọi lớp bài toán với biến ngẫu nhiên liên tục là Hồi quy. Giá trị của nó có thể nằm trong một khoảng hữu hạn ví dụ như thời gian làm bài thi đại học là t∈(0;180) phút hoặc cũng có thể là vô hạn ví dụ như thời gian từ bây giờ đến ngày tận thế t∈(0;+∞) chẳng hạn. Khi đó hàm mật độ xác suất của nó trên toàn miền giá trị D của outcomes space được định nghĩa bằng một tích phân như sau:
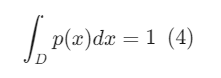
Xác suất có điều kiện
Xác suất có điều kiện là xác suất của một sự kiện xảy ra, biết rằng một sự kiện khác đã xảy ra.
Ví dụ : Gieo lần lượt hai con xúc xắc cân đối và đồng chất. Tính xác suất để tổng số chấm xuất hiện trên hai con xúc xắc bằng 6. Biết rằng con xúc xắc thứ nhất xuất hiện mặt 4 chấm.
Ký hiệu A là biến cố “con xúc xắc thứ nhất xuất hiện mặt 4 chấm” và B là biến cố “ Tổng số chấm xuất hiện trên 2 con xúc xắc bằng 6”. Như vậy A xảy ra trước B.
Khi con xúc xắc xuất hiện mặt 4 chấm (biến cố A đã xảy ra) thì xác suất để tổng số chấm xuất hiện trên hai con xúc xắc bằng 6 được gọi là xác suất điều kiện của biến cố B khi biến cố A đã xảy ra. Ký hiệu là P(B/A). Khi con xúc xắc thứ nhất đã xuất hiện mặt 4 chấm thì không gian mẫu sẽ chỉ còn 6 kết quả (6 biến cố) sau đây: (4,1); (4,2); (4,3); (4,4); (4,5); (4,6). Suy ra P(B/A) = P(4,2)=1/6 .
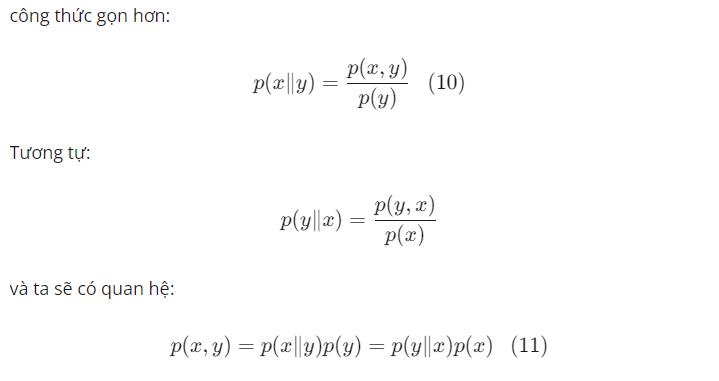
Quy tắc Bayes
Hệ đầy đủ


Công thức bayes
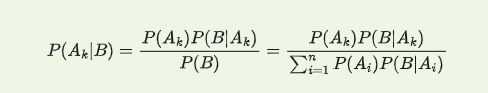
Independence
Nếu biết giá trị của một biến ngẫu nhiên x không mang lại thông tin về việc suy ra giá trị của biến ngẫu nhiên y (và ngược lại), thì ta nói rằng hai biến ngẫu nhiên là độc lập (independence). Chẳng hạn, chiều cao của một học sinh và điểm thi môn Toán của học sinh đó có thể coi là hai biến ngẫu nhiên độc lập.
Khi hai biến ngẫu nhiên x và y là độc lập, ta sẽ có:
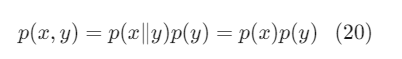
Kỳ vọng
Trong Lý thuyết xác suất, giá trị kỳ vọng, giá trị mong đợi (hoặc kỳ vọng toán học), hoặc trung bình (mean) của một biến ngẫu nhiên là trung bình có trọng số của tất cả các giá trị cụ thể của biến đó, hay là được tính bằng tổng các tích giữa xác suất xảy ra của mỗi giá trị có thể của biến với giá trị đó.
Như vậy, nó biểu diễn giá trị trung bình mà người ta “mong đợi” thắng cược nếu đặt cược liên tục nhiều lần với khả năng thắng cược là như nhau. Lưu ý rằng bản thân giá trị đó có thể không được mong đợi theo nghĩa thông thường; nó có thể ít có khả năng xảy ra hoặc không thể xảy ra. Một trò chơi hoặc một tình huống trong đó giá trị kỳ vọng bằng 0 được gọi là một “trò chơi công bằng” (fair game).
Ví dụ, một vòng quay roulette có 38 kết quả có thể có khả năng như nhau. Mỗi đặt cược vào một số duy nhất thắng 35 (nghĩa là nếu thắng, ta được trả 35 lần số tiền đặt cược; ngược lại mất tiền). Do đó, xét cả 38 kết quả có thể, giá trị kỳ vọng của khoản lợi thu được từ 1 đôla đặt cược cho một số duy nhất là:
nghĩa là khoảng -$0.0526. Do đó, giá trị kỳ vọng là ta sẽ mất trung bình hơn năm xu cho mỗi dola tiền đặt cược.
Một vài phân phối thường gặp
Bernouli distribution
Bernoulli distribution là một phân bố rời rạc mô tả biến ngẫu nhiên nhị phân: nó mô tả trường hợp khi đầu ra chỉ nhận một trong hai giá trị x∈0,1. Hai giá trị này có thể là head và tail khi tung đồng xu; có thể là fraud transaction và normal transaction trong bài toán xác định giao dịch lừa đảo trong tín dụng; có thể là người và không phải người trong bài toán tìm xem trong một bức ảnh có người hay không.
Bernoulli distribution được mô tả bằng một tham số λ∈[0,1] và là xác suất để x=1. Phân bố của mỗi đầu ra sẽ là:
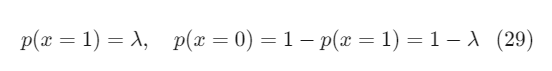
Hai đẳng thức này thường được viết gọn lại:
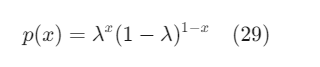
với giả định rằng
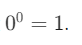
Bernoulli distribution được ký hiệu ngắn gọn dưới dạng:
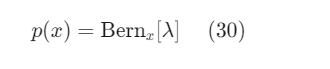
Categorical distribution
Cũng là biến ngẫu nhiên rời rạc, nhưng trong hầu hết các trường hợp, đầu ra có thể là một trong nhiều hơn hai giá trị khác nhau. Ví dụ, một bức ảnh có thể chứa một chiếc xe, một người, hoặc một con mèo. Khi đó, ta dùng phân bố tổng quát của Bernoulli distribution và được gọi là Categorical distribution. Các đầu ra được mô tả bởi 1 phần tử trong tập 1,2,…,K.
Nếu có K đầu ra có thể đạt được, Categorical distribution sẽ được mô tả bởi K tham số, viết dưới dạng vector: λ=[λ1,λ2,…,λK] với các λk không âm và có tổng bằng 1. Mỗi giá trị λk thể hiện xác suất để đầu ra nhận giá trị k:
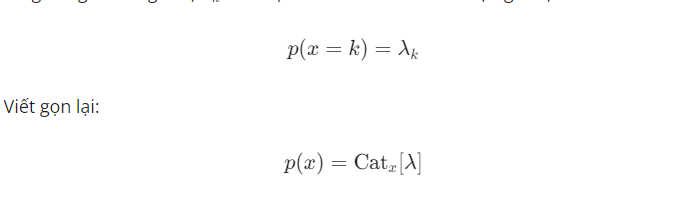
Biểu diễn theo cách khác, ta có thể coi như đầu ra là một vector ở dạng one-hot vector, tức x∈e_1,e_2,…,e_K với e_k là vector đơn vị thứ k, tức tất cả các phần tử bằng 0, trừ phần tử thứ �k bằng 1. Khi đó, ta sẽ có:
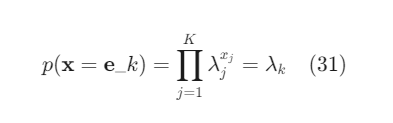
Cách viết này rất thông dụng trong Machine Learning
Đây là một bài viết giới thiệu về lí thuyết xác suất trong Machine Learning. Hiểu và áp dụng chính xác các khái niệm xác suất là một bước quan trọng để xây dựng và đánh giá các mô hình dự đoán hiệu quả. Hy vọng bài viết này đã giúp bạn hiểu rõ hơn về xác suất và cung cấp cho bạn một nền tảng vững chắc để tiếp tục khám phá lĩnh vực Machine Learning.
References: https://viblo.asia/p/ly-thuyet-xac-suat-co-ban-su-dung-trong-machine-learning-naQZR78Plvx




