Merge Sort: Hiểu hơn về thuật toán Merge Sort

Merge Sort là một thuật toán sắp xếp đệ quy, phân chia và trị, được phát triển bởi John von Neumann vào năm 1945. Thuật toán này là một trong những cách phổ biến nhất để sắp xếp một mảng các phần tử. Với hiệu suất O(nlogn) trong trường hợp trường hợp tốt nhất, trung bình và xấu nhất, Merge Sort thường được ưa chuộng khi cần sắp xếp dữ liệu hiệu quả.

1. Cách hoạt động của thuật toán Merge Sort

Vẫn tương tự như bài viết trước ta sẽ cho 1 ví dụ mảng: arr[] = [38, 27, 43, 10]

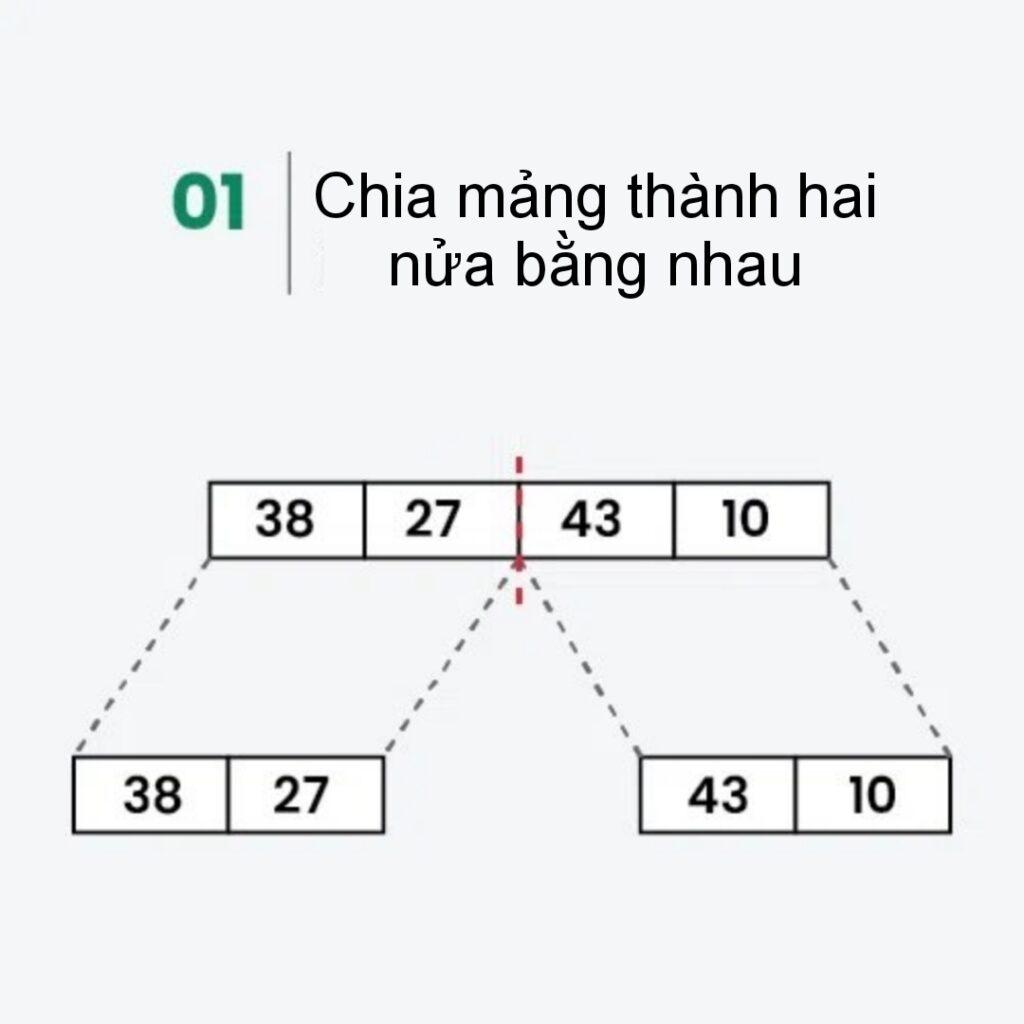
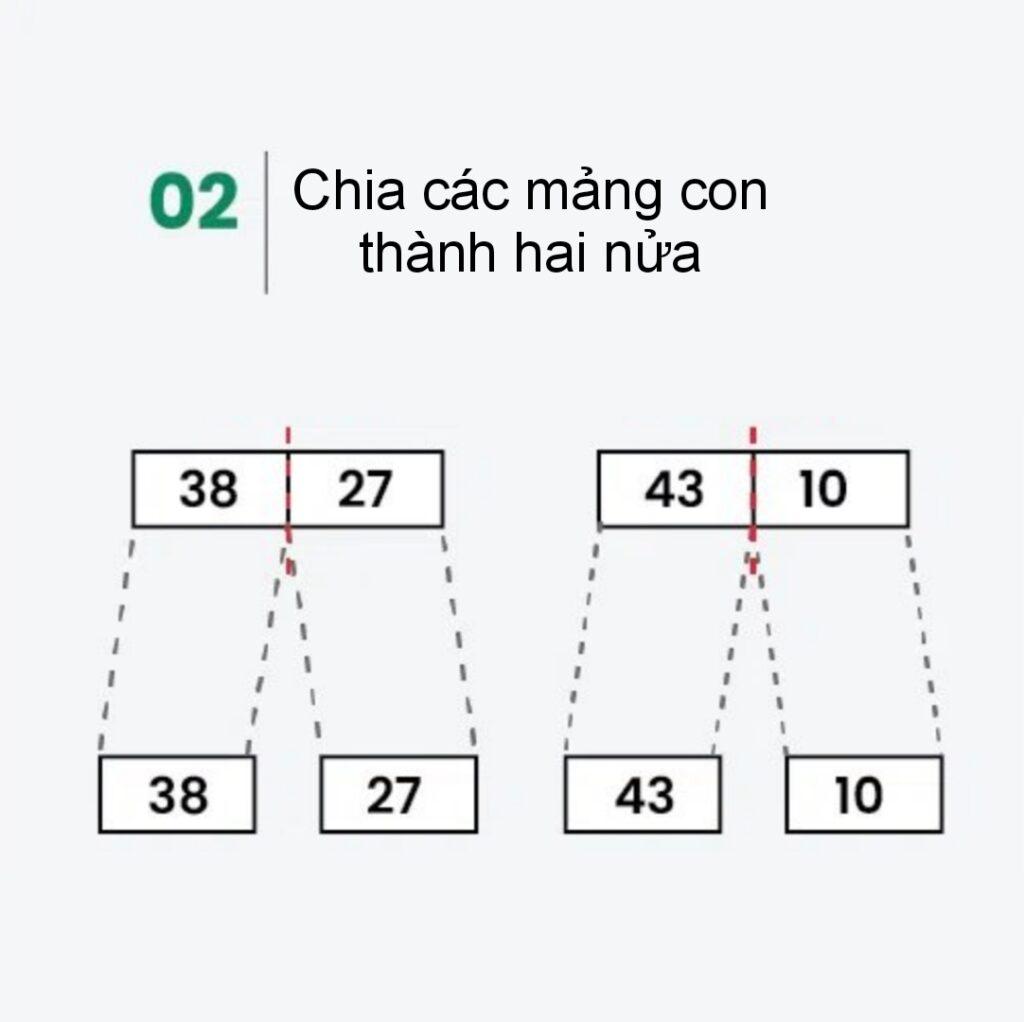
Bước 1: Chia các mảng thành mảng nhỏ

[38, 27, 43, 10] được chia thành [38, 27 ] và [43, 10] .
[38, 27] được chia thành [38] và [27] .
[43, 10] được chia thành [43] và [10] .

Bước 2: Sắp xếp các mảng con

[38] đã được sắp xếp.
[27] đã được sắp xếp.
[43] đã được sắp xếp.
[10] đã được sắp xếp.

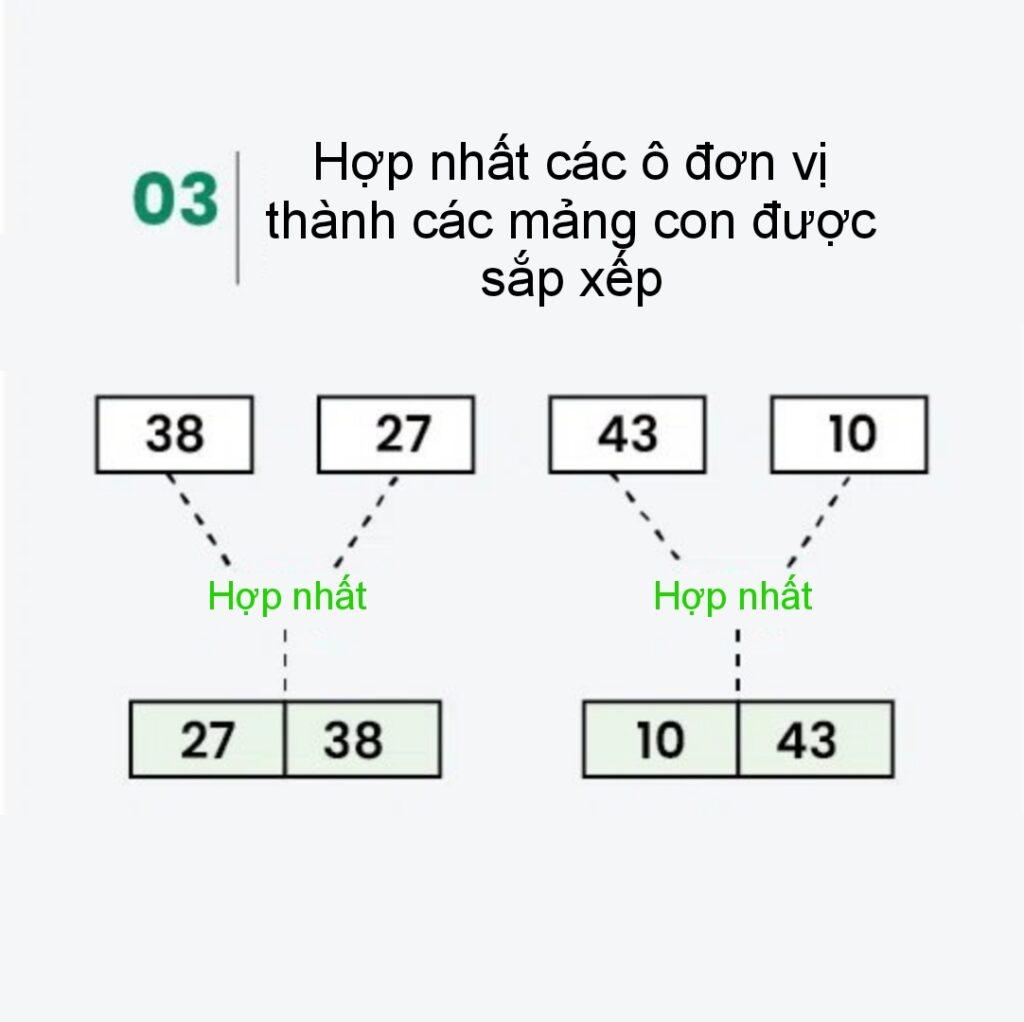
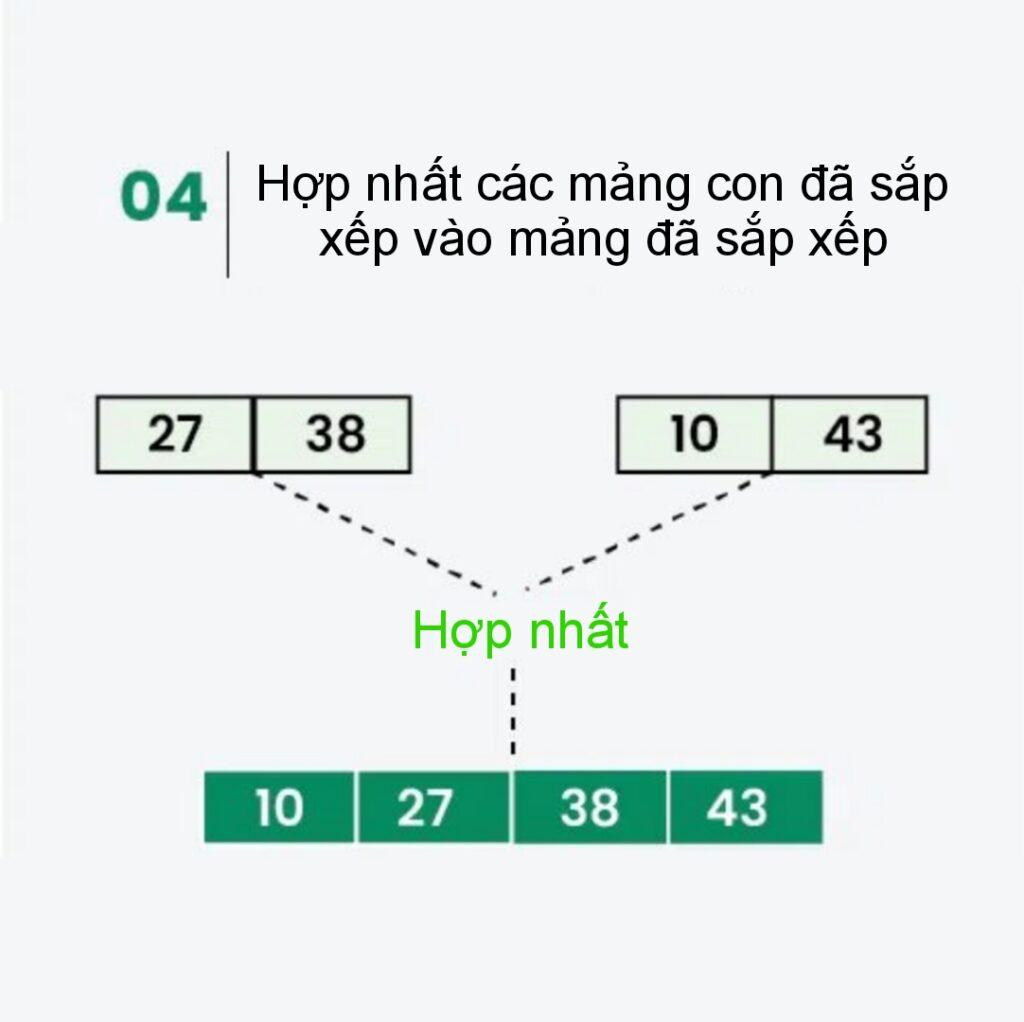
Bước 3: Hợp nhất:

Hợp nhất [38] và [27] để có được [27, 38] .
Hợp nhất [43] và [10] để có được [10,43] .
Hợp nhất [27, 38] và [10,43] để có danh sách được sắp xếp cuối cùng [10, 27, 38, 43]

2. Code thuật toán Merge Sort

function mergeSort(arr) {
    if (arr.length <= 1) {
        return arr; // Trường hợp cơ sở: mảng đã sắp xếp hoặc có một phần tử
    }

    // Phân chia mảng thành hai nửa
    const mid = Math.floor(arr.length / 2);
    const left = arr.slice(0, mid);
    const right = arr.slice(mid);

    // Gọi đệ quy cho mảng con bên trái và bên phải
    const sortedLeft = mergeSort(left);
    const sortedRight = mergeSort(right);

    // Trộn hai mảng đã sắp xếp lại với nhau
    return merge(sortedLeft, sortedRight);
}

function merge(left, right) {
    let result = [];
    let leftIndex = 0;
    let rightIndex = 0;

    // Trộn hai mảng lại với nhau theo thứ tự tăng dần
    while (leftIndex < left.length && rightIndex < right.length) {
        if (left[leftIndex] < right[rightIndex]) {
            result.push(left[leftIndex]);
            leftIndex++;
        } else {
            result.push(right[rightIndex]);
            rightIndex++;
        }
    }

    // Sao chép các phần tử còn lại của mảng trái vào mảng kết quả
    while (leftIndex < left.length) {
        result.push(left[leftIndex]);
        leftIndex++;
    }

    // Sao chép các phần tử còn lại của mảng phải vào mảng kết quả
    while (rightIndex < right.length) {
        result.push(right[rightIndex]);
        rightIndex++;
    }

    return result;
}

// Sử dụng ví dụ:
const arr = [12, 11, 13, 5, 6, 7];
const sortedArr = mergeSort(arr);
console.log("Mảng đã sắp xếp:", sortedArr);

3. Phân tích độ phức tạp của thuật toán Merge Sort

Trường hợp tốt nhất: O(n log n), Khi mảng đã được sắp xếp hoặc gần được sắp xếp.
Trường hợp trung bình: O(n log n), Khi mảng được sắp xếp ngẫu nhiên.
Trường hợp xấu nhất: O(n log n), Khi mảng được sắp xếp theo thứ tự ngược lại.

Độ phức tạp của không gian: O(n), Cần có thêm không gian cho mảng tạm thời được sử dụng trong quá trình hợp nhất.

4. Ưu và nhược điểm của Merge Sort

4.1 Ưu điểm

Tính ổn định : Sắp xếp hợp nhất là một thuật toán sắp xếp ổn định, có nghĩa là nó duy trì thứ tự tương đối của các phần tử bằng nhau trong mảng đầu vào.
Hiệu suất được đảm bảo trong trường hợp xấu nhất: Sắp xếp hợp nhất có độ phức tạp về thời gian trong trường hợp xấu nhất là O(N logN) , có nghĩa là nó hoạt động tốt ngay cả trên các tập dữ liệu lớn.
Thực hiện đơn giản: Cách tiếp cận chia để trị rất đơn giản.

4.2 Nhược điểm

Độ phức tạp về không gian: Sắp xếp hợp nhất yêu cầu bộ nhớ bổ sung để lưu trữ các mảng con đã hợp nhất trong quá trình sắp xếp.
Không đúng chỗ: Sắp xếp hợp nhất không phải là thuật toán sắp xếp tại chỗ, có nghĩa là nó cần thêm bộ nhớ để lưu trữ dữ liệu đã sắp xếp. Đây có thể là một bất lợi trong các ứng dụng mà việc sử dụng bộ nhớ là vấn đề cần quan tâm.

5. Ứng dụng vào thực tế

Sắp xếp các tập dữ liệu lớn
Sắp xếp bên ngoài (khi tập dữ liệu quá lớn để vừa với bộ nhớ)
Đếm nghịch đảo (đếm số lần đảo ngược trong một mảng)
Tìm trung vị của một mảng

6. Kết luận

Merge Sort là một thuật toán hiệu quả cho việc sắp xếp dữ liệu với hiệu suất ổn định và độ phức tạp thời gian O(nlogn). Bằng cách sử dụng phương pháp phân chia và trị, nó có thể sắp xếp mảng với kích thước lớn một cách hiệu quả.

7. Tài liệu

Để hiểu hơn về thuật toán Merge Sort bạn có thể truy cập vào: https://www.geeksforgeeks.org/merge-sort/