Lập trình lượng tử cơ bản với Qiskit

Tổng quan về lượng tử

Lượng tử học là một trong những lĩnh vực khoa học mang tính cách mạng, mở ra cánh cửa cho các công nghệ mới mẻ và tiên tiến như điện toán lượng tử. Trong khi máy tính cổ điển xử lý thông tin dựa trên bit (0 hoặc 1), máy tính lượng tử sử dụng qubit, cho phép biểu diễn trạng thái là sự chồng chất của 0 và 1. Chính điều này mang lại sức mạnh tính toán vượt trội cho các thuật toán phức tạp, đặc biệt là trong lĩnh vực mã hóa, tối ưu hóa, và mô phỏng hệ thống phức tạp.

Lập trình lượng tử là gì?

Lập trình lượng tử là quá trình thiết kế và triển khai các thuật toán lượng tử trên các hệ thống máy tính lượng tử. Các thuật toán này sử dụng các đặc tính cơ bản của cơ học lượng tử như sự chồng chất (superposition), sự rối lượng tử (entanglement), và giao thoa lượng tử (interference) để xử lý thông tin.

Trong lĩnh vực này, Qiskit – một khung phần mềm mã nguồn mở của IBM – là công cụ phổ biến nhất để lập trình lượng tử. Qiskit cung cấp nền tảng mạnh mẽ cho phép các nhà phát triển dễ dàng thiết kế và thử nghiệm các mạch lượng tử.

Mạch cộng bán phần (Half-Adder)

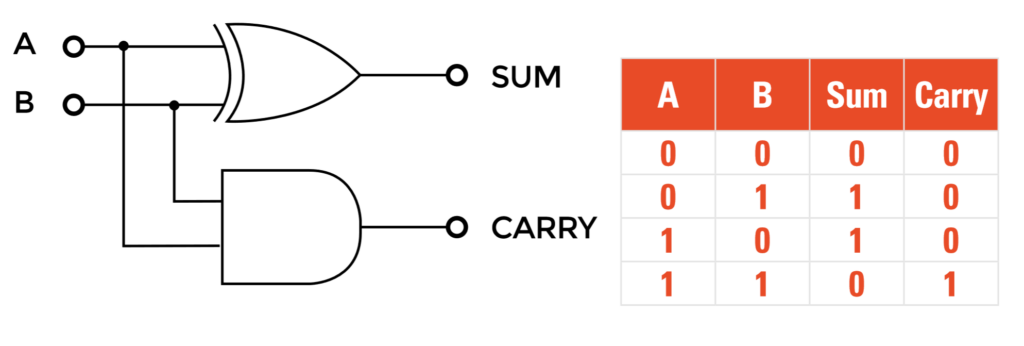
Mạch cộng bán phần (Half-Adder) là một trong những thành phần cơ bản trong các hệ thống số nhị phân, có nhiệm vụ thực hiện phép cộng hai bit nhị phân mà không có bit nhớ (carry-in). Mạch này có thể tính tổng của hai bit đầu vào và cung cấp kết quả dưới dạng bit tổng (sum) và bit nhớ (carry).

Ý tưởng của mạch Half-Adder

Mạch Half-Adder nhận hai bit đầu vào, gọi là A và B. Nó thực hiện phép cộng nhị phân để cho ra hai kết quả:

Bit tổng (sum): Là kết quả của phép cộng giữa A và B.
Bit nhớ (carry): Chỉ ra nếu có một sự phát sinh (carry) trong phép cộng. Với mạch Half-Adder, bit nhớ chỉ có thể là 0 hoặc 1.

Mô hình từ cổng logic

Mạch Half-Adder được xây dựng từ các cổng logic cơ bản:

Cổng XOR: Được sử dụng để tính toán bit tổng. Kết quả sẽ là 1 nếu một trong hai bit đầu vào là 1, nhưng không cả hai.
Cổng AND: Được sử dụng để tính toán bit nhớ. Bit nhớ chỉ có giá trị 1 khi cả hai bit đầu vào đều là 1.

Bảng chân trị của mạch Half-Adder

Input A	Input B	Sum	Carry
0	0	0	0
0	1	1	0
1	0	1	0
1	1	0	1

Phân tích bảng chân trị

Khi cả hai bit đầu vào A và B đều là 0, tổng là 0 và bit nhớ cũng là 0.
Khi chỉ có một trong hai bit đầu vào là 1 (A = 1, B = 0 hoặc A = 0, B = 1), tổng là 1 và bit nhớ là 0.
Khi cả hai bit đầu vào đều là 1, tổng sẽ là 0 (do tính toán nhị phân) và bit nhớ là 1 (đại diện cho sự phát sinh).

Mạch Half-Adder là một phần thiết yếu trong việc xây dựng các mạch cộng phức tạp hơn, như mạch cộng toàn phần (Full-Adder), và nó là cơ sở để hiểu rõ cách hoạt động của các hệ thống số nhị phân.

Mạch cộng lượng tử

Khi bước vào thế giới lượng tử, mạch cộng cổ điển được chuyển thành một mạch cộng lượng tử. Mục tiêu vẫn là thực hiện phép cộng hai bit đầu vào, nhưng thay vì sử dụng các cổng logic cổ điển, chúng ta sử dụng các cổng lượng tử.

Cổng lượng tử cần thiết

CNOT (CX): Đây là cổng điều khiển đảo trạng thái. Nó hoạt động tương tự như cổng XOR trong mạch cổ điển.
Toffoli (CCX): Cổng này là tương đương lượng tử của cổng AND, hoạt động trên ba qubit và được sử dụng để tính toán bit nhớ.

Dưới đây là cách hoạt động của mạch cộng lượng tử:

Tổng: Sử dụng cổng CNOT để tính toán bit tổng của hai qubit đầu vào.
Bit nhớ: Sử dụng cổng Toffoli để tính toán bit nhớ cho phép cộng.

Demo mạch cộng bán phần lượng tử với Qiskit

Chúng ta có thể dễ dàng triển khai mạch cộng bán phần (Half-Adder) lượng tử trên nền tảng Qiskit. Dưới đây là một đoạn mã Python minh họa cách xây dựng mạch cộng lượng tử bằng Qiskit.

from qiskit import QuantumCircuit, transpile, assemble
from qiskit.visualization import plot_histogram
from qiskit_aer import Aer, AerSimulator
from qiskit_aer.primitives import SamplerV2

# Tạo mạch lượng tử với 4 qubit và 2 bit cổ điển
qc = QuantumCircuit(4, 2)

# Giả sử bit đầu vào là a = 1 và b = 1
qc.x(0)  # Đặt qubit a = |1>
qc.x(1)  # Đặt qubit b = |1>

# Tính tổng bằng cổng CNOT
qc.cx(0, 2)
qc.cx(1, 2)

# Tính bit nhớ bằng cổng Toffoli
qc.ccx(0, 1, 3)

# Đo lường kết quả
qc.measure([2, 3], [0, 1])

# Mô phỏng mạch
sim = AerSimulator()
qc = transpile(qc, sim)
qc.draw('mpl')

# Hiển thị kết quả
sampler = SamplerV2()
job = sampler.run([qc])
job_result = job.result()
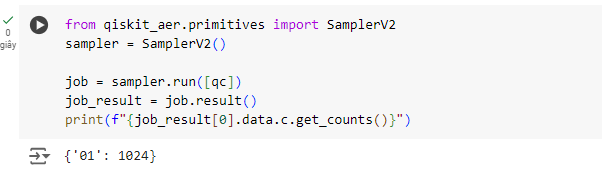
print(f"{job_result[0].data.c.get_counts()}")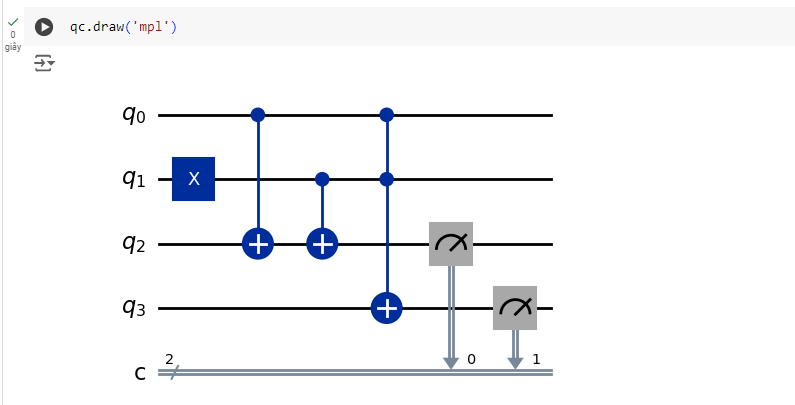

Giải thích

Mạch sử dụng các cổng CNOT và Toffoli để thực hiện phép cộng.
Kết quả cuối cùng được đo lường và trả về dưới dạng bit tổng và bit nhớ, tương tự như cách hoạt động của mạch cộng cổ điển.

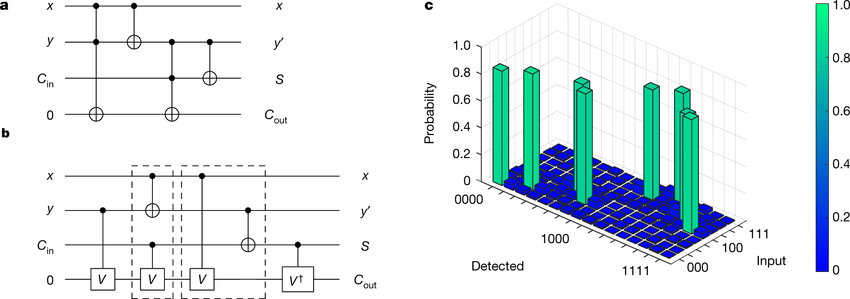
Dưới đây là giải thích chi tiết về từng thành phần trong mạch:

Qubit (q₀, q₁, q₂, q₃)

q₀, q₁, q₂, q₃ là các qubit, trong đó mỗi đường ngang biểu diễn trạng thái của một qubit tại mỗi thời điểm.
c là thanh ghi cổ điển (classical register), dùng để lưu trữ kết quả đo từ qubit.

Cổng X (Pauli-X)

Cổng X (kí hiệu bằng hình vuông có chữ “X”) là một cổng Pauli-X hay còn gọi là cổng NOT trong máy tính cổ điển. Nó lật trạng thái của qubit: biến trạng thái ∣0⟩ thành ∣1⟩ và ngược lại.
Ở đây, cổng X được áp dụng trên qubit q₀ và q₁, biến cả hai qubit từ trạng thái ∣0⟩ thành ∣1⟩.

Cổng CNOT (Controlled-NOT)

Các cổng hình tròn với dấu cộng (+) đại diện cho cổng CNOT (Controlled-NOT gate). CNOT là cổng hai qubit, với một qubit điều khiển và một qubit đích.
- Nếu qubit điều khiển là ∣1⟩, cổng CNOT sẽ đảo trạng thái của qubit đích (nếu là ∣0⟩, nó sẽ trở thành ∣1⟩ và ngược lại).
- Nếu qubit điều khiển là ∣0⟩, qubit đích giữ nguyên trạng thái.
Trong mạch này, các cổng CNOT được điều khiển bởi q₀ và q₁, và tác động lên các qubit q₂ và q₃.
- CNOT đầu tiên: q₀ là qubit điều khiển và q₂ là qubit đích. Nếu q₀ = 1 (như kết quả của cổng X trước đó), trạng thái của q₂ sẽ bị đảo.
- CNOT thứ hai: q₁ là qubit điều khiển và q₂ là qubit đích.
- CNOT thứ ba: q₁ là qubit điều khiển và q₃ là qubit đích.

Cổng đo (Measurement)

Các ô vuông có hình máy đo (ký hiệu đo lường) đại diện cho việc đo các qubit.
Trong mạch này, qubit q₂ và q₃ được đo và kết quả được ghi lại trong thanh ghi cổ điển c, với c[0] ghi kết quả đo của q₂ và c[1] ghi kết quả của q₃.

Hãy áp dụng toàn bộ quá trình mạch lượng tử khi q₀ = 1 và q₁ = 1 để xem cách các qubit thay đổi từ đầu đến cuối:

Trạng thái ban đầu:

Ban đầu, tất cả các qubit giả định là ở trạng thái ∣0⟩:
- q₀ = |0⟩, q₁ = |0⟩, q₂ = |0⟩, q₃ = |0⟩.

Bước 1: Áp dụng cổng X trên q₀ và q₁

Cổng X trên q₀ và q₁ chuyển cả hai qubit này từ ∣0⟩ thành ∣1⟩.
- Sau cổng X:
  - q₀ = |1⟩
  - q₁ = |1⟩
  - q₂ = |0⟩ (giả định)
  - q₃ = |0⟩ (giả định)

Bước 2: Áp dụng CNOT số 1 (q₀ là điều khiển, q₂ là đích)

CNOT số 1 sử dụng q₀ làm qubit điều khiển và q₂ là qubit đích:
- q₀ = 1, do đó trạng thái của q₂ bị đảo từ ∣0⟩ thành ∣1⟩.
- Sau CNOT số 1:
  - q₀ = |1⟩
  - q₁ = |1⟩
  - q₂ = |1⟩
  - q₃ = |0⟩

Bước 3: Áp dụng CNOT số 2 (q₁ là điều khiển, q₂ là đích)

CNOT số 2 sử dụng q₁ làm qubit điều khiển và q₂ là qubit đích:
- q₁ = 1, nên trạng thái của q₂ sẽ bị đảo lần nữa từ ∣1⟩ thành ∣0⟩.
- Sau CNOT số 2:
  - q₀ = |1⟩
  - q₁ = |1⟩
  - q₂ = |0⟩ (trở lại trạng thái ban đầu)
  - q₃ = |0⟩

Bước 4: Áp dụng Cổng Toffoli (CCNOT) trên q₀ và q₁ (q₃ là đích)

Cổng Toffoli yêu cầu cả hai qubit điều khiển q₀ và q₁ đều phải bằng ∣1⟩ để đảo trạng thái của q₃.
- Ở đây, cả q₀ = 1 và q₁ = 1, do đó trạng thái của q₃ bị đảo từ ∣0⟩ thành ∣1⟩.
- Sau cổng Toffoli:
  - q₀ = |1⟩
  - q₁ = |1⟩
  - q₂ = |0⟩
  - q₃ = |1⟩

Bước 5: Đo q₂ và q₃

q₂ và q₃ được đo và kết quả được lưu trữ vào thanh ghi cổ điển c:
- c[0] ghi kết quả đo của q₂ (kết quả là 0).
- c[1] ghi kết quả đo của q₃ (kết quả là 1).

Kết quả cuối cùng của mạch:

q₀ = 1, q₁ = 1, q₂ = 0, q₃ = 1.
Kết quả đo được lưu vào thanh ghi cổ điển: c[0] = 0, c[1] = 1.

Tóm tắt diễn biến của mạch:

Cổng X biến q₀ và q₁ thành |1⟩.
CNOT số 1 đảo q₂ thành |1⟩.
CNOT số 2 lại đảo q₂ quay về |0⟩.
Cổng Toffoli đảo q₃ thành |1⟩ khi cả q₀ và q₁ đều bằng |1⟩.
Đo q₂ và q₃, kết quả là q₂ = 0 và q₃ = 1.

Bạn có thể tham khảo link Google Colab sau của tôi: https://colab.research.google.com/drive/1lZN0jXbz9xOuY1vOA8AgdR-cVe5ihIc1#scrollTo=tSCg1TZUcT7H

Kết Luận

Mạch cộng lượng tử là một trong những khối xây dựng cơ bản trong các thuật toán lượng tử. Việc hiểu rõ cách chuyển đổi từ mạch cộng cổ điển sang mạch cộng lượng tử giúp chúng ta nắm bắt tốt hơn sự khác biệt giữa máy tính cổ điển và lượng tử.

Hãy tiếp tục theo dõi để khám phá thêm nhiều ứng dụng thú vị của lập trình lượng tử với Qiskit!

Lập trình lượng tử cơ bản với Qiskit – P1: Mạch cộng