Cho một cây N-ary có N nút được đánh số từ 0 đến N-1 và danh sách các cạnh vô hướng, nhiệm vụ là tìm (các) nút ở tâm của cây đã cho.
Trước khi tìm hiểu cách tìm nút ở giữa của cây ta cần hiểu một vài thuật ngữ sau:
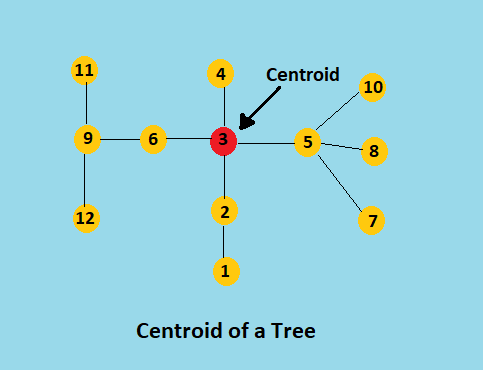
- Độ lệch tâm: Độ lệch tâm của bất kỳ đỉnh V nào trong một cây nhất định là khoảng cách tối đa giữa đỉnh V đã cho và bất kỳ đỉnh nào khác của cây.
- Tâm: Tâm của cây là đỉnh có độ lệch tâm nhỏ nhất.
Vây, để tìm được tâm chúng ta phải giảm thiểu độ lệch tâm này.
Ví dụ:
Đầu vào:
- N = 4,
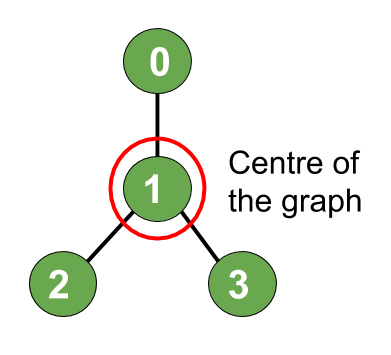
- Cạnh[] = { (1, 0), (1, 2), (1, 3)}
Đầu ra: 1
Giải thích:
Đầu vào:
- N = 6,
- Cạnh[] = { (0, 3), (1, 3), (2, 3), (4, 3), (5, 4)}
Đầu ra: 3, 4
Giải thích:
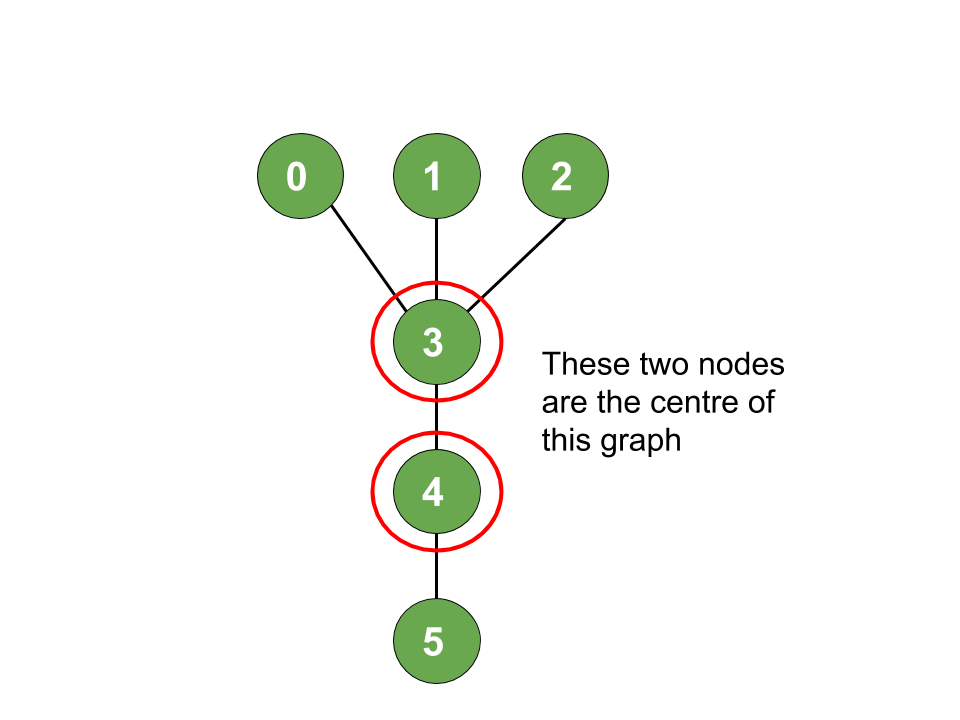
Có thể quan sát thấy đường đi có độ lệch tâm cực đại là đường kính của cây. Do đó, tâm của đường kính cây cũng sẽ là tâm của cây.
- Nếu đường kính bao gồm số nút lẻ thì chỉ tồn tại 1 tâm.
- Nếu đường kính bao gồm số nút chẵn thì có 2 nút trung tâm.
- Độ phức tạp về thời gian: O(N)
- Không gian phụ trợ: O(N)
Dưới đây là cách thực hiện phương pháp trên với c++:
Hàm thêm cạnh giữa 2 điểm
void addedge(int a, int b)
{
tree[a].push_back(b);
tree[b].push_back(a);
}Hàm lấy và trả về nút xa nhất từ một đỉnh nhất định
void farthestNode(int vertex, int parent,
int height, int& maxHeight,
int& maxHeightNode)
{
if (height > maxHeight) {
maxHeight = height;
maxHeightNode = vertex;
}
for (auto i : tree[vertex]) {
if (i == parent)
continue;
farthestNode(i, vertex,
height + 1,
maxHeight,
maxHeightNode);
}
}Hàm lưu trữ đường đi từ đỉnh đã cho đến đỉnh đích trong đường dẫn vectơ
bool getDiameterPath(int vertex,
int targetVertex,
int parent,
vector<int>& path)
{
if (vertex == targetVertex) {
path.push_back(vertex);
return true;
}
for (auto i : tree[vertex]) {
if (i == parent)
continue;
if (getDiameterPath(i, targetVertex,
vertex, path)) {
path.push_back(vertex);
return true;
}
}
return false;
}Hàm tìm node trung tâm
void FindCenter(int n)
{
int maxHeight = -1;
int maxHeightNode = -1;
farthestNode(0, -1, 0, maxHeight,
maxHeightNode);
int leaf1 = maxHeightNode;
maxHeight = -1;
farthestNode(maxHeightNode,
-1, 0, maxHeight,
maxHeightNode);
int leaf2 = maxHeightNode;
vector<int> path;
getDiameterPath(leaf1, leaf2,
-1, path);
int pathSize = path.size();
if (pathSize % 2) {
cout << path[pathSize / 2]
<< endl;
}
else {
cout << path[pathSize / 2]
<< ", "
<< path[(pathSize - 1) / 2]
<< endl;
}
}Kết hợp code
#include <bits/stdc++.h>
using namespace std;
void addedge(int a, int b)
{
tree[a].push_back(b);
tree[b].push_back(a);
}
void farthestNode(int vertex, int parent,
int height, int& maxHeight,
int& maxHeightNode)
{
if (height > maxHeight) {
maxHeight = height;
maxHeightNode = vertex;
}
for (auto i : tree[vertex]) {
if (i == parent)
continue;
farthestNode(i, vertex,
height + 1,
maxHeight,
maxHeightNode);
}
}
bool getDiameterPath(int vertex,
int targetVertex,
int parent,
vector<int>& path)
{
if (vertex == targetVertex) {
path.push_back(vertex);
return true;
}
for (auto i : tree[vertex]) {
if (i == parent)
continue;
if (getDiameterPath(i, targetVertex,
vertex, path)) {
path.push_back(vertex);
return true;
}
}
return false;
}
void FindCenter(int n)
{
int maxHeight = -1;
int maxHeightNode = -1;
farthestNode(0, -1, 0, maxHeight,
maxHeightNode);
int leaf1 = maxHeightNode;
maxHeight = -1;
farthestNode(maxHeightNode,
-1, 0, maxHeight,
maxHeightNode);
int leaf2 = maxHeightNode;
vector<int> path;
getDiameterPath(leaf1, leaf2,
-1, path);
int pathSize = path.size();
if (pathSize % 2) {
cout << path[pathSize / 2]
<< endl;
}
else {
cout << path[pathSize / 2]
<< ", "
<< path[(pathSize - 1) / 2]
<< endl;
}
}
map<int, vector<int> > tree;
int main()
{
int N = 4;
addedge(1, 0);
addedge(1, 2);
addedge(1, 3);
FindCenter(N);
return 0;
}Tài liệu tham khảo: Find the node at center