Nén dữ liệu là quá trình giảm kích thước của tập tin hoặc dữ liệu mà không làm mất đi nội dung gốc. Quá trình này giúp tiết kiệm không gian lưu trữ và tăng tốc độ truyền tải dữ liệu qua mạng
1. Huffman Coding
Mã hóa Huffman là một thuật toán mã hóa dùng để nén dữ liệu. Nó dựa trên bảng tần suất xuất hiện các ký tự cần mã hóa để xây dựng một bộ mã nhị phân cho các ký tự đó sao cho dung lượng (số bit) sau khi mã hóa là nhỏ nhất.
1.1. Mã tiền tố (Prefix code)
Để mã hóa các ký hiệu (ký tự, chữ số,…) ta thay chúng bằng các xâu nhị phân, được gọi là từ mã của ký hiệu đó. Chẳng hạn bộ mã ASCII, mã hóa cho 256 ký hiệu là biểu diễn nhị phân của các số từ 0 đến 255, mỗi từ mã gồm 8 bit. Trong ASCII từ mã của ký tự “a” là 1100001, của ký tự “A” là 1000001. Trong cách mã hóa này các từ mã của tất cả 256 ký hiệu có độ dài bằng nhau (mỗi từ mã 8 bit). Nó được gọi là mã hóa với độ dài không đổi.
Khi mã hóa một tài liệu có thể không sử dụng đến tất cả 256 ký hiệu. Hơn nữa trong tài liệu chữ cái “a” chỉ có thể xuất hiện 1000000 lần còn chữ cái “A” có thể chỉ xuất hiện 2, 3 lần. Như vậy ta có thể không cần dùng đủ 8 bit để mã hóa cho một ký hiệu, hơn nữa độ dài (số bít) dành cho mỗi ký hiệu có thể khác nhau, ký hiệu nào xuất hiện nhiều lần thì nên dùng số bit ít, ký hiệu nào xuất hiện ít thì có thể mã hóa bằng từ mã dài hơn. Như vậy ta có việc mã hóa với độ dài thay đổi. Tuy nhiên, nếu mã hóa với độ dài thay đổi, khi giải mã ta làm thế nào phân biệt được xâu bít nào là mã hóa của ký hiệu nào. Một trong các giải pháp là dùng các dấu phẩy (“,”) hoặc một ký hiệu quy ước nào đó để tách từ mã của các ký tự đứng cạnh nhau. Nhưng như thế số các dấu phẩy sẽ chiếm một không gian đáng kể trong bảng mã. Một cách giải quyết khác dẫn đến khái niệm mã tiền tố
Mã tiền tố là bộ các từ mã của một tập hợp các ký hiệu sao cho từ mã của mỗi ký hiệu không là tiền tố (phần đầu) của từ mã một ký hiệu khác trong bộ mã ấy.
Đương nhiên mã hóa với độ dài không đổi là mã tiền tố.
Ví dụ: Giả sử mã hóa từ “ARRAY”, tập các ký hiệu cần mã hóa gồm 3 chữ cái “A”,”R”,”Y”.
Nếu mã hóa bằng các từ mã có độ dài bằng nhau ta dùng ít nhất 2 bit cho một chữ cái chẳng hạn “A”=00, “R”=01, “Y”=10. Khi đó mã hóa của cả từ là 0001010010. Để giải mã ta đọc hai bit một và đối chiếu với bảng mã.
Nếu mã hóa “A”=0, “R”=01, “Y”=11 thì bộ từ mã này không là mã tiền tố vì từ mã của “A” là tiền tố của từ mã của “R”. Để mã hóa cả từ ARRAY phải đặt dấu ngăn cách vào giữa các từ mã 0,01,01,0,11
Nếu mã hóa “A”=0, “R”=10, “Y”=11 thì bộ mã này là mã tiền tố. Với bộ mã tiền tố này khi mã hóa xâu “ARRAY” ta có 01010011.
2. Giải thuật
Với ý tưởng trên, thuật toán Huffman coding gồm 3 bước:
Bước 1: Đếm tần suất xuất hiện của các phần tử trong chuỗi đầu vào.
Bước 2: Xây dựng cây Huffman (cây nhị phân mã hóa).
Bước 3: Từ cây Huffman, ta có được các giá trị mã hóa. Lúc này, ta có thể xây dựng chuỗi mã hóa từ các giá trị này.
Quá trình xây dựng cây Huffman gồm các bước sau:
2.1. Tạo danh sách chứa các nút lá bao gồm phần tử đầu vào và trọng số nút là tần suất xuất hiện của nó.
2.2. Từ danh sách này, lấy ra 2 phần tử có tần suất xuất hiện ít nhất. Sau đó gắn 2 nút vừa lấy ra vào một nút gốc mới với trọng số là tổng của 2 trọng số ở nút vừa lấy ra để tạo thành một cây.
2.3. Đẩy cây mới vào lại danh sách.
2.4. Lặp lại bước 2 và 3 cho đến khi danh sách chỉ còn 1 nút gốc duy nhất của cây.
2.5. Nút còn lại chính là nút gốc của cây Huffman.
Giả sử chúng ta có chuỗi dữ liệu cần nén là “Hellooo!”.
Bước 2.1: Sau khi đếm tần suất xuất hiện các phần tử đầu vào. Chúng ta tạo danh sách các nút lá với trọng số là tần suất xuất hiện. Danh sách sẽ có 5 phần tử như bên dưới.
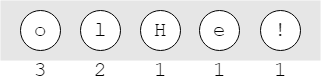
Bước 2.2 và 2.3: Chọn 2 nút có trọng số thấp nhất, tạo nút gốc mới có trọng số bằng tổng 2 trọng số nút con. Sau đó gắn 2 nút con vào nút gốc và đẩy lại vào danh sách. Danh sách cần được biểu diễn đặc biệt để có thể lấy ra các nút trọng số nhỏ nhất một cách tối ưu nhất.
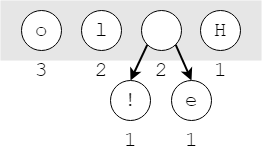
Bước 2.4: Lặp lại các bước 2.2 và 2.3.
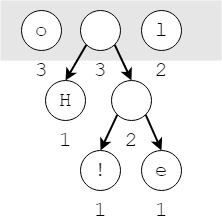
lần 1
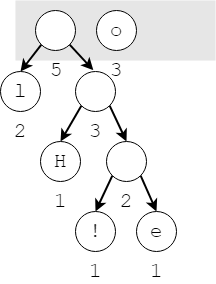
lần 2
Bước 2.5: Chỉ còn lại 1 nút trong danh sách, nút này chính là cây Huffman
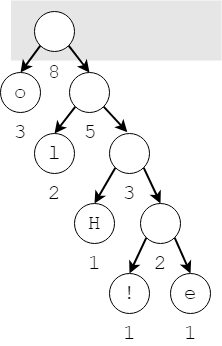
Từ cây Huffman, ta có thể suy ra các giá trị mã hóa của từng phần tử bằng cách duyệt cây nhị phân mã hóa.
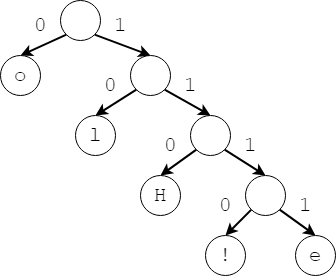
Chuỗi mã hóa Huffman của “Hellooo!” sẽ là: 000000010101111001
Tham khảo:
https://en.wikipedia.org/wiki/Huffman_coding




