Heap Sort: Hiểu về thuật toán sắp xếp Heap

Heap Sort là một thuật toán sắp xếp dựa trên cấu trúc dữ liệu cây nhị phân gọi là heap. Thuật toán này sử dụng một heap tối đa (max-heap) hoặc heap tối thiểu (min-heap) để sắp xếp các phần tử của mảng. Heap Sort có độ phức tạp thời gian O(n log n) và không yêu cầu bộ nhớ bổ sung đáng kể, làm cho nó trở thành một lựa chọn hiệu quả và ổn định cho nhiều bài toán sắp xếp.

1. Cách hoạt động của thuật toán Heap Sort

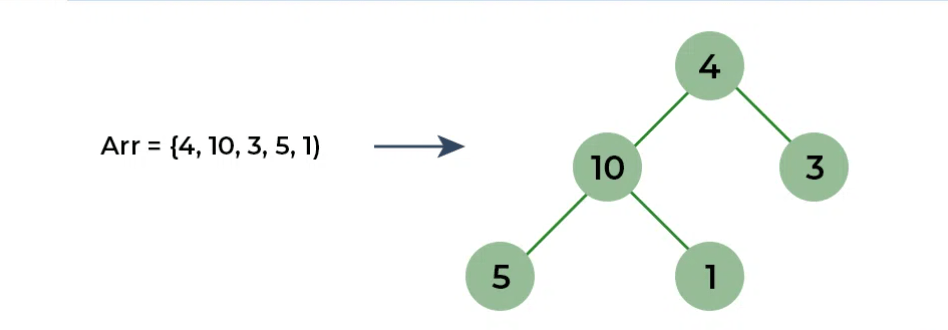
Giả sử ta có mảng cần sắp xếp arr = [4, 10, 3, 5, 1]

Bước 1: Xây dựng heap

• Chuyển đổi mảng thành một max-heap. Bắt đầu từ nút không lá sâu nhất, áp dụng quy trình heapify để duy trì tính chất max-heap.
• Xây dựng max-heap từ arr:
  • arr = [4, 10, 3, 5, 1] Bắt đầu từ nút không lá cuối cùng: – heapify(3): không thay đổi vì 5 > 1. – heapify(1): 10 là phần tử lớn nhất, không thay đổi. – heapify(0): 10 là phần tử lớn nhất, hoán đổi 10 và 4: arr = [10, 4, 3, 5, 1]
• Tiếp tục áp dụng heapify để duy trì max-heap:
  • heapify(1): 5 > 4, hoán đổi 5 và 4: arr = [10, 5, 3, 4, 1]

Bước 2: Thực hiện sắp xếp heap

Loại bỏ phần tử tối đa trong mỗi bước (tức là di chuyển nó đến vị trí cuối cùng và loại bỏ phần tử đó), sau đó xem xét các phần tử còn lại và chuyển nó thành heap tối đa.

• Xóa phần tử gốc (10) khỏi vùng heap tối đa. Để xóa nút này, hãy thử hoán đổi nó với nút cuối cùng, tức là (1). Sau khi loại bỏ phần tử gốc, hãy gộp lại phần tử đó để chuyển nó thành vùng heap tối đa.
  • Heap và mảng kết quả sẽ trông như thế này:

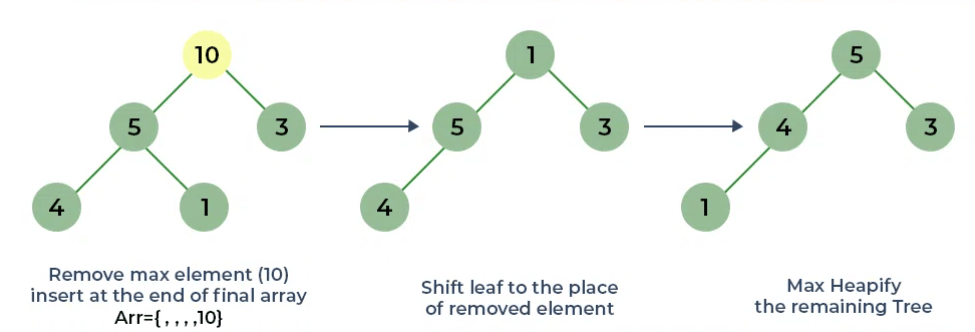
Bước 3: Loại bỏ phần tử lớn nhất khỏi root và tối đa hóa Heap

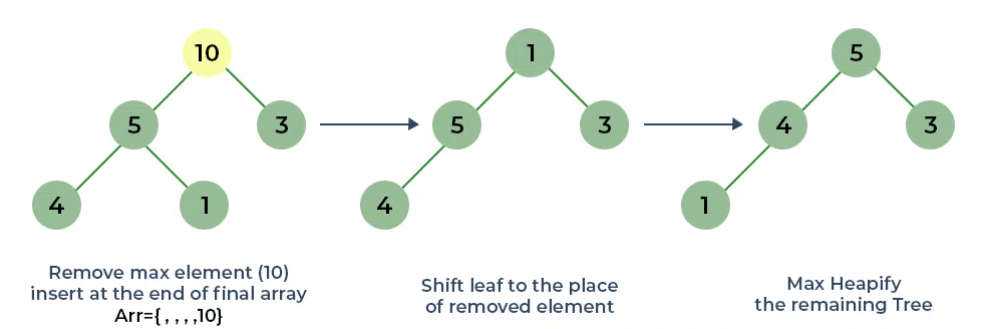
Bước 4: Loại bỏ phần tử lớn nhất kế tiếp khỏi root và tối đa hóa Heap

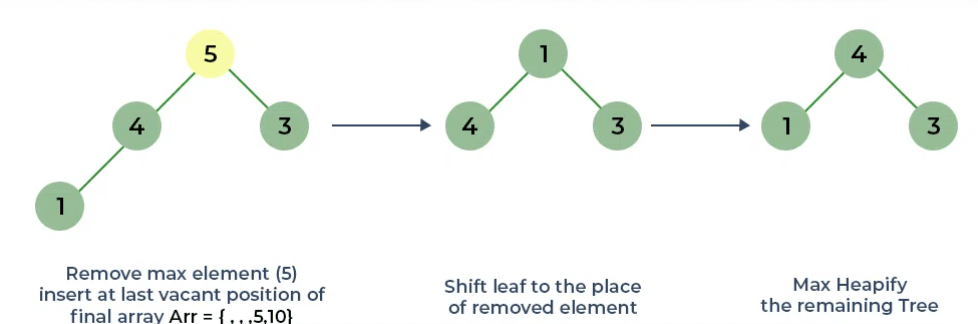
Bước 5: Tiếp tục loại bỏ phần tử lớn nhất kế tiếp khỏi root và tối đa hóa Heap

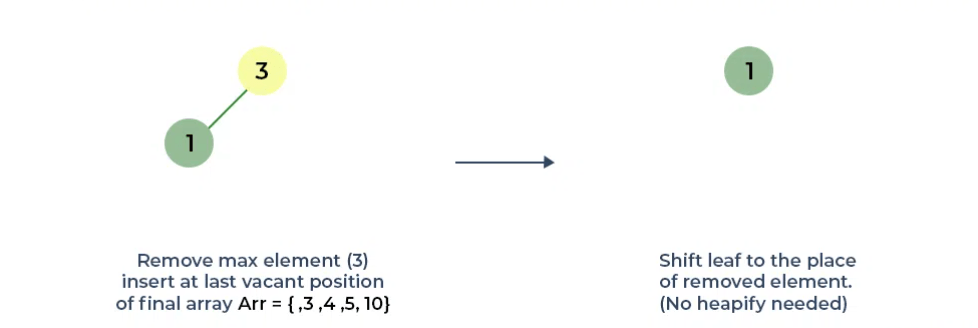
Bước 6: Tiếp tục loại bỏ, ta sẽ được 1 mảng được sắp xếp

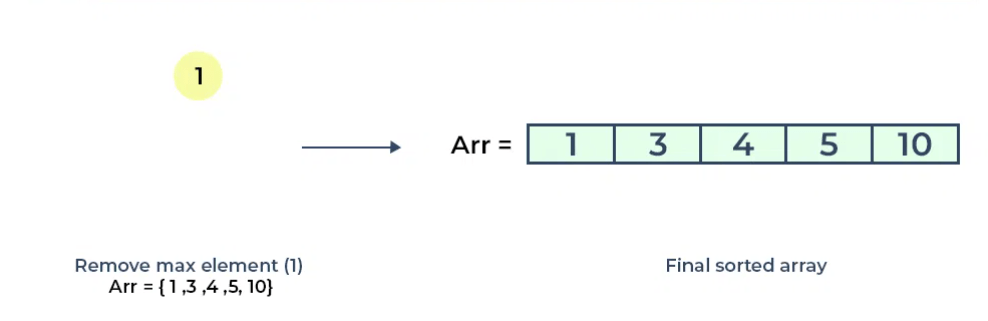
2. Code thuật toán Heap Sort

function heapify(arr, n, i) {
    let largest = i;  // Khởi tạo largest là gốc
    let left = 2 * i + 1;  // left = 2*i + 1
    let right = 2 * i + 2;  // right = 2*i + 2

    // Nếu left lớn hơn gốc
    if (left < n && arr[left] > arr[largest])
        largest = left;

    // Nếu right lớn hơn largest hiện tại
    if (right < n && arr[right] > arr[largest])
        largest = right;

    // Nếu largest không phải là gốc
    if (largest != i) {
        [arr[i], arr[largest]] = [arr[largest], arr[i]];  // Hoán đổi

        // Đệ quy heapify cây con bị ảnh hưởng
        heapify(arr, n, largest);
    }
}

function heapSort(arr) {
    let n = arr.length;

    // Xây dựng heap (rearrange array)
    for (let i = Math.floor(n / 2) - 1; i >= 0; i--)
        heapify(arr, n, i);

    // Trích xuất từng phần tử một từ heap
    for (let i = n - 1; i > 0; i--) {
        // Di chuyển gốc hiện tại đến cuối
        [arr[0], arr[i]] = [arr[i], arr[0]];

        // gọi max heapify trên heap giảm dần
        heapify(arr, i, 0);
    }
}

// Example usage:
let arr = [4, 10, 3, 5, 1];
console.log("Original array:", arr);
heapSort(arr);
console.log("Sorted array:", arr);

3. Phân tích độ phức tạp của thuật toán Heap Sort

Độ phức tạp về thời gian: O(N log N)
Không gian phụ trợ: O(log n), do ngăn xếp cuộc gọi đệ quy. Tuy nhiên, không gian phụ trợ có thể là O(1) để thực hiện lặp lại.

4. Ưu và nhược điểm của Heap Sort

4.1 Ưu điểm

• Độ phức tạp về thời gian hiệu quả: Sắp xếp đống có độ phức tạp về thời gian là O(n log n) trong mọi trường hợp. Điều này làm cho việc sắp xếp các tập dữ liệu lớn trở nên hiệu quả. Hệ số log n xuất phát từ chiều cao của đống nhị phân và nó đảm bảo rằng thuật toán duy trì hiệu suất tốt ngay cả với số lượng lớn phần tử.
• Sử dụng bộ nhớ – Việc sử dụng bộ nhớ có thể ở mức tối thiểu (bằng cách viết một heapify() lặp thay vì đệ quy). Vì vậy, ngoài những gì cần thiết để giữ danh sách các mục ban đầu cần được sắp xếp, nó không cần thêm dung lượng bộ nhớ để hoạt động.
• Tính đơn giản –  Nó dễ hiểu hơn các thuật toán sắp xếp hiệu quả tương đương khác vì nó không sử dụng các khái niệm khoa học máy tính tiên tiến như đệ quy.

4.2 Nhược điểm

• Tốn kém : Sắp xếp đống tốn kém vì các hằng số cao hơn so với sắp xếp hợp nhất ngay cả khi độ phức tạp về thời gian là O(n Log n) cho cả hai.
• Không ổn định : Sắp xếp heap không ổn định. Nó có thể sắp xếp lại thứ tự tương đối.
• Hiệu quả: Sắp xếp Heap không hiệu quả lắm khi làm việc với dữ liệu có độ phức tạp cao. 

5. Ứng dụng vào thực tế

• Không cần bộ nhớ bổ sung: Heap Sort là một thuật toán sắp xếp tại chỗ (in-place), không yêu cầu bộ nhớ bổ sung đáng kể ngoài mảng đầu vào.
• Ổn định: Heap Sort không phải là một thuật toán sắp xếp ổn định. Phần tử có giá trị bằng nhau có thể bị thay đổi thứ tự tương đối.

6. Kết luận

Heap Sort là một thuật toán sắp xếp hiệu quả và mạnh mẽ với độ phức tạp thời gian O(n log n) và không yêu cầu bộ nhớ bổ sung đáng kể. Nó đặc biệt hữu ích khi cần một thuật toán sắp xếp tại chỗ và không yêu cầu tính ổn định. Heap Sort thường được sử dụng trong các ứng dụng yêu cầu hiệu suất cao và sử dụng hiệu quả bộ nhớ, chẳng hạn như trong các hệ thống nhúng và các hệ thống có hạn chế về tài nguyên.

7. Tài liệu tham khảo

Để hiểu hơn về thuật toán Cycle Sort bạn có thể truy cập vào: https://www.geeksforgeeks.org/heap-sort/