1. Giới thiệu
Dynamic programming (quy hoạch động) là một kỹ thuật được sử dụng rộng rãi trong lĩnh vực IT để giải quyết các bài toán tối ưu. Phương pháp này dựa trên việc tận dụng các kết quả trung gian đã được tính toán trước đó để giảm thiểu số lần tính toán lặp lại và cải thiện hiệu suất giải thuật. Trong bài viết này, chúng ta sẽ đi vào chi tiết về dynamic programming và cách áp dụng nó vào các bài toán thực tế.
2. Đặc điểm của dynamic programming
Quy hoạch động có một số đặc điểm quan trọng:
2.1. Tính chồng chéo
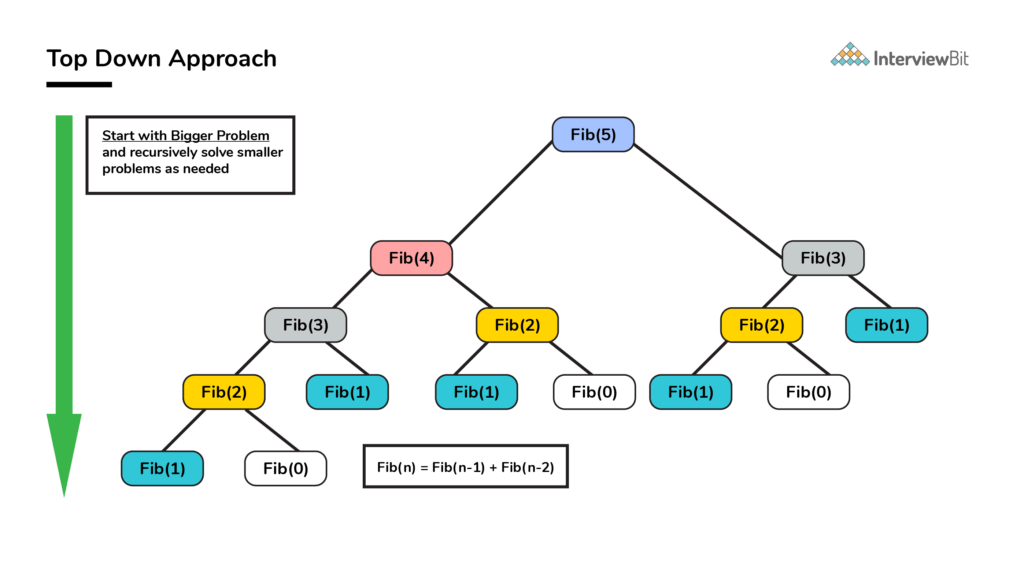
Dynamic programming thường áp dụng cho các bài toán có cấu trúc chồng chéo, trong đó các lời giải của các phần con được lưu trữ và sử dụng lại để tạo ra lời giải của phần lớn hơn. Điều này giúp giảm bớt thời gian tính toán so với việc tính toán lại từ đầu.
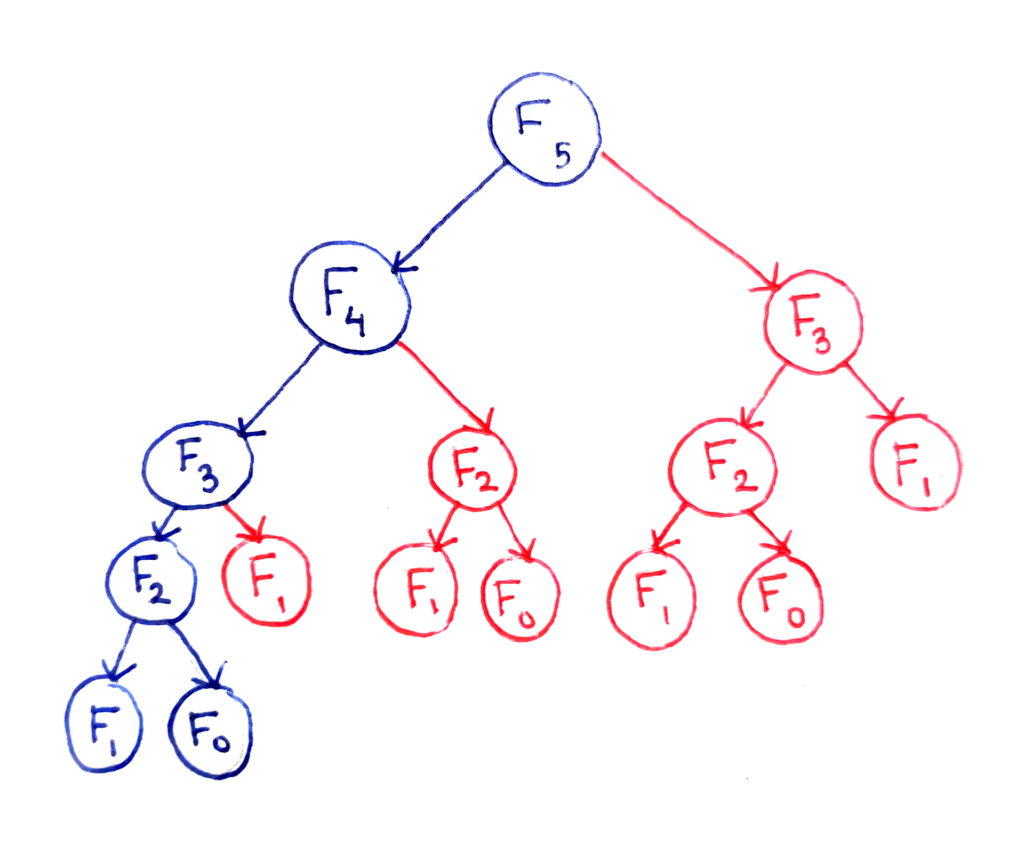
Một ví dụ điển hình: Bài toán tính số fibonacci thứ n
2.2. Quy tắc Bellman
Bellman là một công cụ quan trọng trong dynamic programming, giúp tính toán các lời giải tối ưu cho bài toán. Quy tắc này dựa trên việc tìm kiếm và cập nhật các giá trị tối ưu thông qua việc thử và so sánh các lời giải khác nhau.
3. Các bước thực hiện dynamic programming
Để áp dụng dynamic programming vào việc giải quyết bài toán, chúng ta có thể tuân theo các bước sau:
3.1. Xác định cấu trúc chồng chéo
Trước hết, chúng ta cần phân tích bài toán và xác định cấu trúc chồng chéo của nó. Điều này giúp chúng ta nhìn thấy quy tắc lặp và các bước chồng chéo trong quá trình giải quyết.
3.2. Định nghĩa hàm trạng thái
Tiếp theo, chúng ta định nghĩa hàm trạng thái, biểu diễn trạng thái của bài toán bằng một hàm. Hàm này sẽ lưu trữ các giá trị tối ưu hoặc thông tin liên quan đến việc giải quyết bài toán.
3.3. Quy tắc chuyển tiếp
Quy tắc chuyển tiếp là quy tắc để tính toán các giá trị tối ưu của hàm trạng thái dựa trên các giá trị trạng thái trước đó. Chúng ta áp dụng quy tắc này để cập nhật giá trị tối ưu và tiến đến lời giải cuối cùng.
4. Ví dụ về dynamic programming
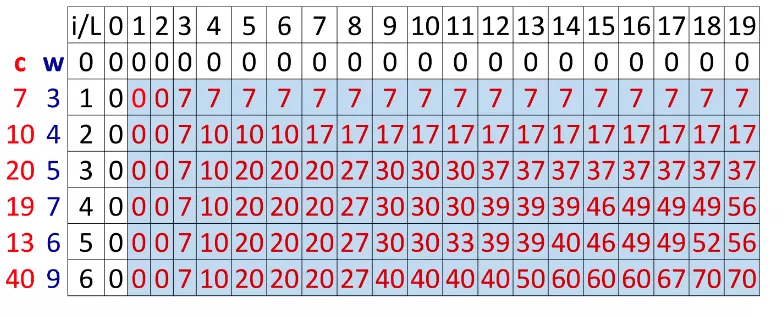
Để minh họa cho việc áp dụng dynamic programming, chúng ta có thể xem xét bài toán cái túi (knapsack problem). Bài toán này yêu cầu chọn một tập hợp các đồ vật có giá trị và trọng lượng khác nhau để đặt vào một cái túi có trọng lượng tối đa.
Áp dụng dynamic programming, chúng ta có thể sử dụng bảng 2 chiều để lưu trữ các giá trị tối ưu cho các trọng lượng con và đồ vật con. Quy tắc chuyển tiếp sẽ giúp chúng ta cập nhật các giá trị tối ưu trong bảng dựa trên các giá trị trạng thái trước đó.
Phân tích bài toán có:
n– Số đồ vật,- b – trọng lượng túi (lấy giá trị nguyên)
Phân rã: Với các giá trị
i(1..n)vàL(0..b)GọiMaxV(i,L)là tổng giá trị lớn nhất có thể chọn trongiđồ vật (từ1đếni) với trọng lượng tối đa của túi làL. Khi đóMaxV(n,b)là giá trị lớn nhất mang đi được.Giải bài toán con:
MaxV(0,L) = 0với mọiL, vàMaxV(i,0) = 0với mọii.Tổng hợp:
- Đã có
MaxV(i-1,L): Giá trị lớn nhất mang đi được vớii-1đồ vật khi trọng lượng túi làL.- Xét đồ vật thứ i khi trọng lượng túi vẫn là
L: Chỉ mang thêm đồ vật thứikhi giá trị của túi lúc mangi-1đồ vật ở trọng lượng túi làL - w * i(như thế mới đảm bảo mang thêm được đồ vật i có trọng lượngW_ikhi trọng lượng túi làL) cộng với giá trị của đồ vật thứi,c[i]lớn hơn khi không mang đồ vật thứi,MaxV(i-1,L).- Nghĩa là: MaxV(i,L)=MaxMaxV(i−1,L−w[i])+c[i],MaxV(i−1,L)
Kết luận
Dynamic programming là một kỹ thuật quan trọng trong lĩnh vực IT, giúp giải quyết các bài toán tối ưu một cách hiệu quả. Bằng cách tận dụng các kết quả trung gian đã tính toán trước đó, chúng ta có thể giảm thiểu số lần tính toán lặp lại và đạt được hiệu suất tốt hơn trong việc giải quyết bài toán. Việc áp dụng dynamic programming đòi hỏi phân tích cấu trúc chồng chéo, định nghĩa hàm trạng thái và sử dụng quy tắc chuyển tiếp. Với những ưu điểm và công dụng của nó, dynamic programming xứng đáng là một kỹ thuật quan trọng mà mọi lập trình viên nên biết đến.