Dẫn nhập
Các bài toán về đồ thị luôn là những bài toán khó và hóc búa với các lập trình viên. Một trong những kiến thức cơ bản nhất về đồ thị chính là Disjoint Sets Union. Hãy cùng tìm hiểu nó trong bài viết này nhé!
Nội dung cần thiết để hiểu về Disjoint Sets Union
Để có thể tiếp thu bài viết này một cách tốt nhất, các bạn nên có những kiến thức cơ bản về:
- Đồ thị và cây
- BFS và DFS
- Các bài viết khác về Thuật toán
Bài toán đặt ra
Một công ty có n máy tính được đánh số từ 1 đến n. Ban đầu, các máy tính là độc lập và không có kết nối với nhau. Biết rằng 2 máy tính được xem là có kết nối với nhau nếu chúng được cắm dây mạng trực tiếp với nhau hoặc thông qua kết nối với các máy tính khác.
Có q truy vấn thuộc 1 trong 2 loại sau:
: Nối 2 máy tính
và
bằng dây mạng
: Kiểm tra xem có tồn tại kết nối từ máy tính
đến máy tính
hay không. Nếu có in ra “YES”, ngược lại in ra “NO”
Input:
- Dòng 1: Hai số nguyên dương n và q thể hiện cho số máy tính và số truy vấn
- Dòng 2…q+1: Mỗi dòng là một truy vấn thuộc 1 trong 2 dạng trên
Output:
- Với mỗi truy vấn loại 2, in ra “YES” nếu tồn tại kết nối giữa 2 máy, ngược lại in ra “NO”
Ví dụ:
| Input | Output |
| 6 8 U 2 3 U 3 5 Q 5 2 U 1 4 Q 1 2 U 1 3 U 2 4 Q 2 1 | YES NO YES |
Nhận xét
Bài toán này nếu làm theo suy nghĩ thông thường để giải sẽ khá khó khăn và phức tạp. Do đó, ta sẽ cần một cách tiếp cận bài toán mới.
Tiếp cận
Ta sẽ coi mỗi máy tính là một đỉnh của một đồ thị có hướng. Ban đầu, mỗi đỉnh sẽ tồn tại một khuyên.

Khi ta thực hiện thao tác kết nối máy tính x và máy tính y, thay vì cạnh có hướng từ đỉnh x trỏ đến chính nó, ta sẽ chỉnh cạnh có hướng đó trỏ vào đỉnh y. Ví dụ như ở trong ví dụ trên, khi ta kết nối máy tính 2 vào máy tính 3 ta sẽ có đồ thị như sau:

Khi ta kết nối máy tính 3 và máy tính 5 ta sẽ có đồ thị như sau:

Đó là xây dựng hệ thống kết nối giữa các máy tính. Vậy làm sao để kiểm tra xem giữa 2 máy tính có kết nối trực tiếp (bằng dây mạng) hoặc gián tiếp (thông qua việc kết nối với các máy tính trung gian khác) hay không?
Giải pháp
Ta nhận thấy rằng, nếu như các máy tính được kết nối với nhau thì các đỉnh đại diện cho chúng sẽ có chung gốc.
Ví dụ:
- Đỉnh 2 có gốc là đỉnh 5 do có đường đi từ đỉnh 2 đến đỉnh 3, từ đỉnh 3 đến đỉnh 5 và không tồn tại đường đi đến đỉnh nào khác nữa.
- Đỉnh 3 có gốc là đỉnh 5 do có đường đi từ đỉnh 3 đến đỉnh 5 và không tồn tại đường đi đến đỉnh nào khác.
Do đó, đỉnh 2 và đỉnh 3 có chung gốc hay có nghĩa là tồn tại kết nối từ máy tính 2 đến máy tính 3.
Tiếp tục, khi ta kết nối máy 1 và máy 4 ta sẽ có đồ thị như sau:

Khi này, ta thấy gốc của đỉnh 1 là đỉnh 4, gốc của đỉnh 2 là đỉnh 5 nên không tồn tại kết nối giữa hai máy 1 và 5.
Tổng hợp
Tiếp tục, ta kết nối máy 1 và máy 3. Khi này, ta sẽ tạo một cạnh có hướng từ đỉnh gốc của đỉnh 1 đến đỉnh gốc của đỉnh 3. Tại sao lại vậy?
Ta thấy rằng do các kết nối là 2 chiều nên nếu tồn tại kết nối giữa máy 1 với máy 3 thì cũng sẽ tồn tại các kết nối giữa máy 1 với máy 2 và máy 5 (do máy 3 kết nối với máy 2 và máy 15). Tương tự, cũng sẽ tồn tại kết nối giữa máy 4 với các máy 2 và 5.
Nói cách khác, nếu như hai máy trong hai tập khác nhau được kết nối với nhau thì tất cả các máy trong hai tập sẽ được kết nối với nhau. Do đó, ta sẽ nối đỉnh gốc của hai tập để thể hiện hai tập này được kết nối với nhau.
Khi đó, đồ thị ta có như sau:

Chú ý: Ở trong đồ thị trên mình tạo cạnh nối đỉnh 4 vào đỉnh 5 tuy nhiên nếu các bạn nối đỉnh 5 vào đỉnh 4 thì vẫn đúng. Chiều của cạnh nối trong DSU không ảnh hưởng đến kết quả.
Tiếp theo, ta cần kết nối máy 1 và máy 4. Ta thấy, hai đỉnh đại diện cho 2 máy khi này đã chung gốc là đỉnh 5 nên việc kết nối 2 máy không gây ảnh hưởng gì đến đồ thị.
Lúc này, đỉnh 1 và đỉnh 2 chung gốc nên tồn tại kết nối giữa máy 1 và máy 2.
Toàn bộ những ý tưởng mà mình trình bày ở trên chính là ý tưởng của Disjoint Sets Union.
Tổng quan về Disjoint Sets Union
Khái niệm
Disjoint Sets Union (gọi tắt là DSU) là một cấu trúc dữ liệu chứa nhiều phần tử được phân chia vào các tập hợp khác nhau. DSU có thể gộp hai tập hợp cũng như cho biết một phần tử thuộc tập hợp nào.
Phương thức cơ bản của Disjoint Sets Union
Một DSU sẽ hỗ trợ các phương thức cơ bản sau:
- Tạo tập hợp chứa các phần tử
- Gộp hai tập hợp chứa hai phần tử yêu cầu lại làm một
- Tìm kiếm tập hợp chứa phần tử yêu cầu
Xây dựng Disjoint Sets Union
Nguyên tắc
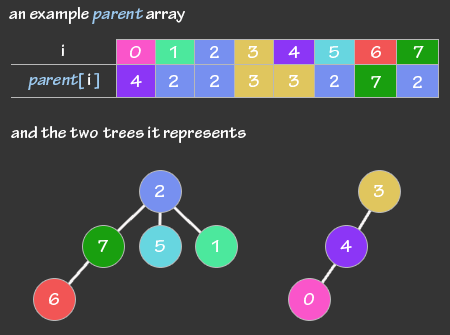
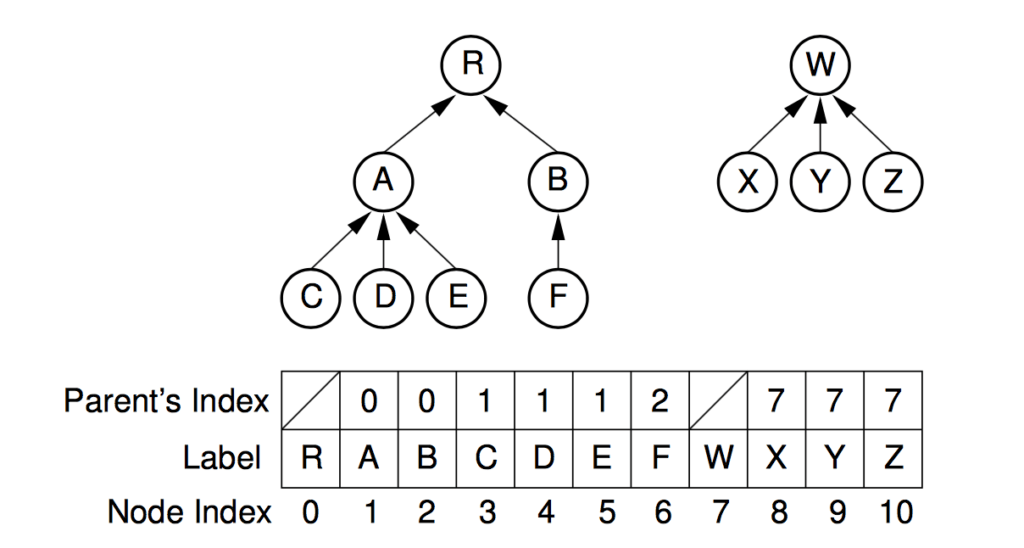
Thông thường, DSU sẽ được xây dựng dưới dạng một đồ thị có hướng như mình đã trình bày ở phần trên. Để thể hiện cạnh có hướng nối từ đỉnh này đến đỉnh khác, ta sẽ dùng một mảng parent với ý nghĩa parent[u] = v là tồn tại cạnh có hướng nối từ đỉnh u đến đỉnh v.
Để khởi tạo tập hợp chứa các phần tử, ta đơn giản chỉ cần tạo ra một cây có đỉnh là chính phần tử đó.
Nếu muốn gộp hai tập hợp chứa hai phần tử yêu cầu lại làm một, trước hết ta sẽ phải tìm xem đỉnh gốc của hai tập hợp chứa hai phần tử của hai phần tử đã cho rồi sau đó, gán cha của một đỉnh là đỉnh còn lại.
Ngoài ra, để tìm tập hợp chứa phần tử yêu cầu, ta chỉ cần đi theo cha của đỉnh đó tới khi đến đỉnh gốc (đỉnh có cha là chính nó)
Code ban đầu (Disjoint Sets Union)
#include<bits/stdc++.h>
using namespace std;
const int MaxN = 1 + 1e6;
int n, q, parent[MaxN];
void make_set(int u){
parent[u] = u;
}
int find_set(int u){
if(u == parent[u]) return u;
return find_set(parent[u]);
}
void union_set(int u, int v){
u = find_set(u);
v = find_set(v);
if(u == v) return;
parent[u] = v;
}
int main(){
freopen("CTDL.inp","r",stdin);
freopen("CTDL.out","w",stdout);
cin >> n >> q;
for(int i = 1 ; i <= n ; ++i) make_set(i);
while(q--){
char query;
int x, y;
cin >> query >> x >> y;
if(query == 'Q'){
if(find_set(x) == find_set(y)) cout << "YES" << endl;
else cout << "NO" << endl;
}
else{
union_set(x, y);
}
}
return 0;
}
Cải tiến
Ta thấy trong code trên, nếu như cây suy biến thành đường thẳng thì hàm find_set() sẽ mất độ phức tạp và nếu như hàm được gọi lại nhiều lần thì chương trình của chúng ta sẽ chậm. Do đó, ta sẽ cần phải cải tiến hàm này.
Ta lại thấy với mỗi đỉnh ta chỉ quan tâm đến đỉnh gốc của đỉnh đó. Do đó, trong quá trình tìm kiếm đỉnh gốc, ta sẽ gán cha của tất cả các đỉnh trên đường đi về đỉnh gốc.
Code khi này sẽ như sau:
Code mẫu 2 (Disjoint Sets Union)
#include<bits/stdc++.h>
using namespace std;
const int MaxN = 1 + 1e6;
int n, q, parent[MaxN];
void make_set(int u){
parent[u] = u;
}
int find_set(int u){
if(u == parent[u]) return u;
return parent[u] = find_set(parent[u]);
}
void union_set(int u, int v){
u = find_set(u);
v = find_set(v);
if(u == v) return;
parent[u] = v;
}
int main(){
freopen("CTDL.inp","r",stdin);
freopen("CTDL.out","w",stdout);
cin >> n >> q;
for(int i = 1 ; i <= n ; ++i) make_set(i);
while(q--){
char query;
int x, y;
cin >> query >> x >> y;
if(query == 'Q'){
if(find_set(x) == find_set(y)) cout << "YES" << endl;
else cout << "NO" << endl;
}
else{
union_set(x, y);
}
}
return 0;
}
Khi này, hàm find_set() có độ phức tạp trung bình sẽ là .
Kết luận
- Qua bài này chúng ta đã nắm về Disjoint Set. Cảm ơn các bạn đã theo dõi bài viết. Hãy để lại bình luận hoặc góp ý của mình để phát triển bài viết tốt hơn.