CTDL Disjoint Sets Union

Cấu trúc dữ liệu Disjoint Sets (hay còn gọi là Union-Find) là một phương pháp quản lý tập hợp các phần tử để theo dõi và thao tác với các tập rời rạc. Nó được sử dụng rộng rãi trong các bài toán đồ thị, như kiểm tra chu trình hoặc xây dựng cây khung tối thiểu (Minimum Spanning Tree).

1. Disjoint Sets là gì?

Disjoint Sets quản lý nhiều tập hợp rời rạc, trong đó mỗi phần tử thuộc duy nhất một tập. Hai thao tác chính là:

• Find(x): Xác định tập chứa phần tử x.
• Union(x, y): Hợp nhất hai tập chứa x và y.

2. Nguyên lý hoạt động

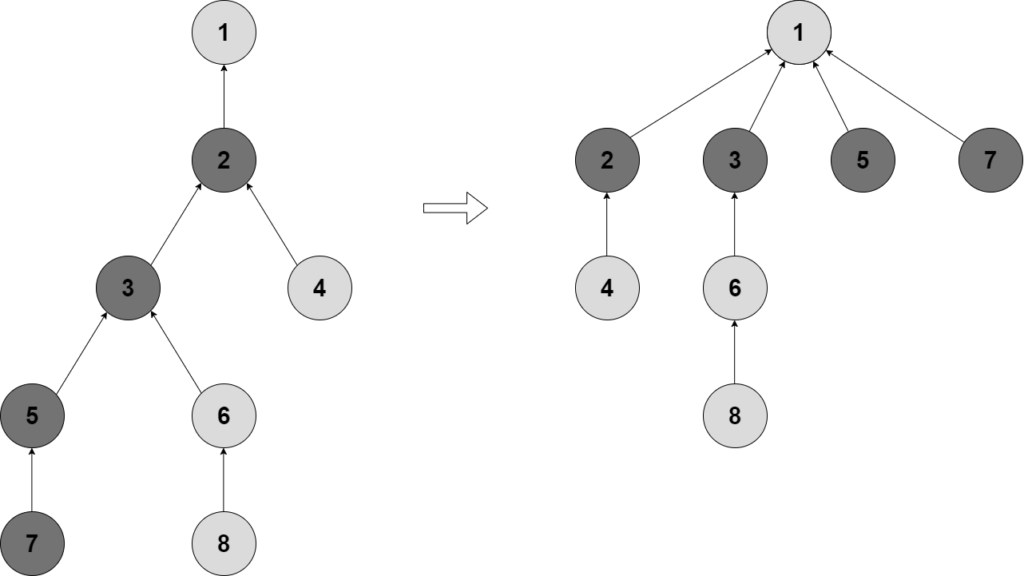
Thuật toán Disjoint Sets dùng câu trúc dữ liệu cây để quản lý các tập rời rạc:

1. Mỗi tập được biểu diễn bởi một cây, trong đó gốc cây đại diện cho tập.
2. Thành viên của tập được liên kết với gốc qua một chuỗi các nút trung gian.

Hai kỹ thuật quan trọng trong Disjoint Sets giúp tối ưu hoá hoạt động là:

• Path Compression: Rút ngắn đường dẫn đến gốc bằng cách liên kết trực tiếp tất cả các nút trong chuỗi với gốc.
• Union by Rank: Gắn cây có chiều cao thấp hơn vào cây có chiều cao lớn hơn.

3. Cài đặt thuật toán Disjoint Sets bằng Python

Dưới đây là mã giả minh họa:

class DisjointSet:
    def __init__(self, n):
        self.parent = [i for i in range(n)]
        self.rank = [0] * n

    def find(self, x):
        if self.parent[x] != x:
            self.parent[x] = self.find(self.parent[x])  # Path compression
        return self.parent[x]

    def union(self, x, y):
        root_x = self.find(x)
        root_y = self.find(y)

        if root_x != root_y:
            if self.rank[root_x] > self.rank[root_y]:
                self.parent[root_y] = root_x
            elif self.rank[root_x] < self.rank[root_y]:
                self.parent[root_x] = root_y
            else:
                self.parent[root_y] = root_x
                self.rank[root_x] += 1

# Ví dụ sử dụng
ds = DisjointSet(5)
ds.union(0, 1)
ds.union(1, 2)
print(ds.find(2))  # Output: 0
print(ds.find(3))  # Output: 3

4. Phân tích độ phức tạp

• Find: O(α(n)), với α là hàm ngược Ackermann, rất nhỏ trong thực tế.
• Union: O(α(n)).

5. Ưứng dụng trong thực tế

• Kiểm tra chu trình trong đồ thị.
• Thuật toán Kruskal: Xây dựng cây khung tối thiểu.
• Quản lý các tập phần tử trong bài toán nhóm.

6. Kết luận

Thuật toán Disjoint Sets là công cụ hiệu quả cho các bài toán quản lý tập hợp rời rạc. Nhờ vào Path Compression và Union by Rank, thuật toán đáp ứng yêu cầu hiệu suất cao trong các bài toán quy mô lớn.