Counting Sort: Hiểu về thuật toán sắp xếp Đếm

Counting Sort là một thuật toán sắp xếp không so sánh, có hiệu quả với các mảng có giá trị phần tử nằm trong phạm vi hữu hạn và không quá lớn. Thuật toán này đặc biệt hữu ích khi cần sắp xếp các mảng có phần tử là số nguyên hoặc các ký tự có thể ánh xạ tới số nguyên.

1. Cách hoạt động của thuật toán Counting Sort

Đầu tiên cũng sẽ cho mảng = [2,5,3,0,2,3,0,3]

Bước 1: Tìm số lớn nhất

Như ta thấy mảng trên phần tử 5 là phần tử có giá trị lớn nhất

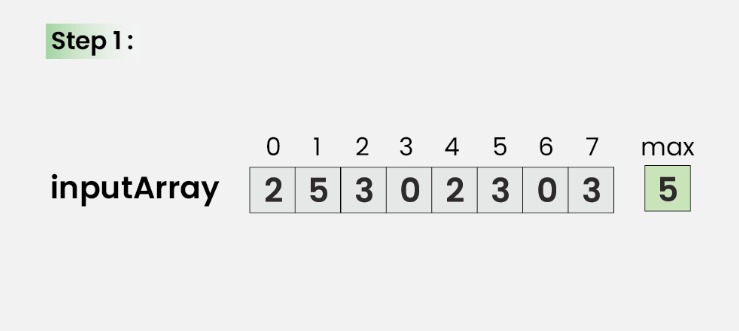
Bước 2: Khởi tạo 1 mảng countArray có độ dài `max + 1`

Ở đây ta thấy giá trị lớn nhất là 5 thì ta sẽ lấy 5 + 1. Các phần tử sẽ bắt đầu bằng 0 . Mảng này sẽ được sử dụng để lưu trữ lần xuất hiện của các phần tử của mảng đầu vào.

Bước 3: Trong countArray[] , lưu trữ số lượng từng phần tử duy nhất của mảng đầu vào tại các chỉ mục tương ứng của chúng.

Ví dụ: Số lượng phần tử 2 trong mảng đầu vào là 2. Vì vậy, hãy lưu trữ 2 ở chỉ mục 2 trong countArray[] . Tương tự, số phần tử 5 trong mảng đầu vào là 1 , do đó lưu trữ 1 ở chỉ mục 5 trong countArray[] .

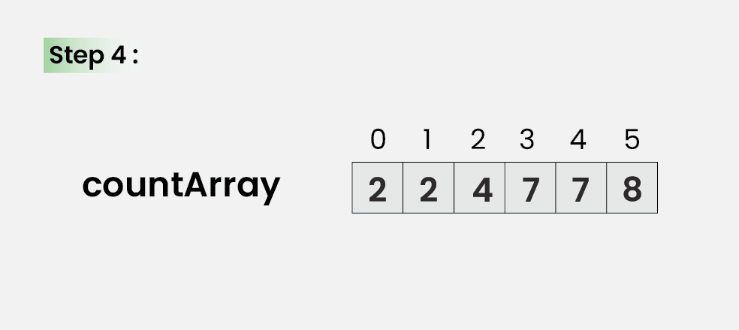
Bước 4: Lưu trữ tổng tích lũy hoặc tổng tiền tố của các phần tử

Bằng cách thực hiện countArray[i] = countArray[i – 1] + countArray[i]. Điều này sẽ giúp đặt các phần tử của mảng đầu vào vào đúng chỉ mục trong mảng đầu ra.

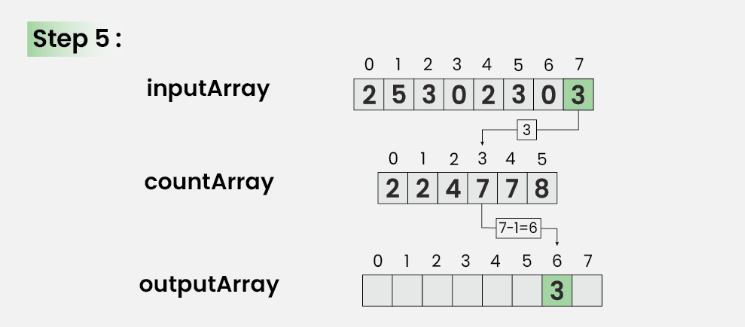
Bước 5: Lặp lại từ cuối mảng đầu vào và vì việc duyệt qua mảng đầu vào từ cuối sẽ giữ nguyên thứ tự của các phần tử bằng nhau, điều này cuối cùng làm cho thuật toán sắp xếp này ổn định.

• Cập nhật outArray[ countArray[ inputArray[i] ] – 1] = inputArray[i] .
• Ngoài ra, hãy cập nhật countArray[ inputArray[i] ] = countArray[ inputArray[i] ] – -.

Bước 6: Với i = 6

Cập nhật outArray[ countArray[ inputArray[6] ] – 1] = inputArray[6]
Ngoài ra, cập nhật countArray[ inputArray[6] ] = countArray[ inputArray[6] ]- –

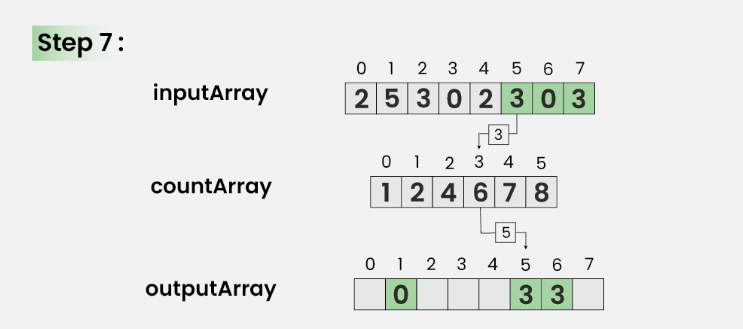
Bước 7: Với i = 5

Cập nhật outArray[ countArray[ inputArray[5] ] – 1] = inputArray[5]
Ngoài ra, cập nhật countArray[ inputArray[5] ] = countArray[ inputArray[5] ]- –

Bước 8: Với i = 4

Cập nhật outArray[ countArray[ inputArray[4] ] – 1] = inputArray[4]
Ngoài ra, cập nhật countArray[ inputArray[4] ] = countArray[ inputArray[4] ]- –

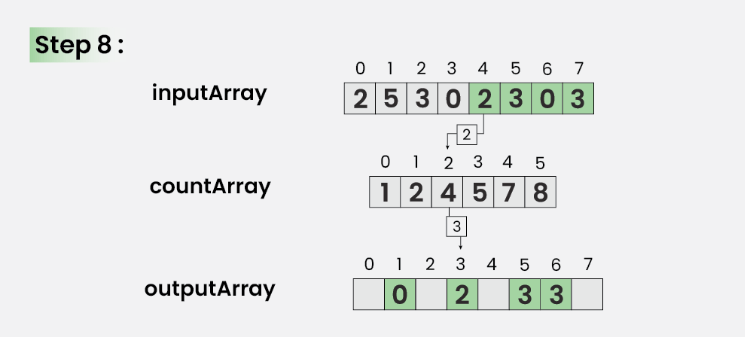
Bước 9: Với i = 3

Cập nhật outArray[ countArray[ inputArray[3] ] – 1] = inputArray[3]
Ngoài ra, cập nhật countArray[ inputArray[3] ] = countArray[ inputArray[3] ]- –

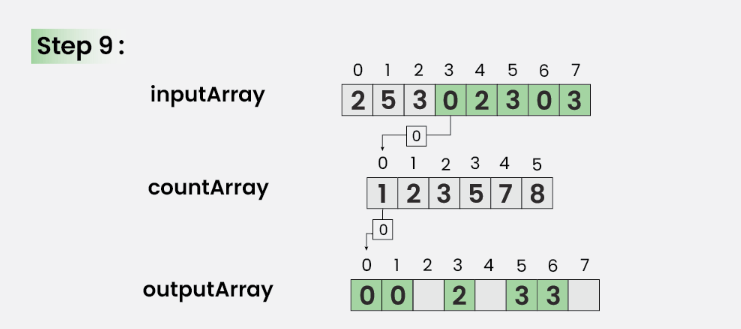
Bước 10: Với i = 2

Cập nhật outArray[ countArray[ inputArray[2] ] – 1] = inputArray[2]
Ngoài ra, cập nhật countArray[ inputArray[2] ] = countArray[ inputArray[2] ]- –

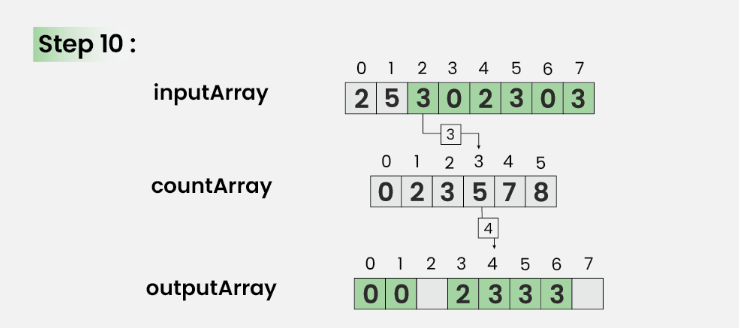
Bước 11: Với i = 1

Cập nhật outArray[ countArray[ inputArray[1] ] – 1] = inputArray[1]
Ngoài ra, cập nhật countArray[ inputArray[1] ] = countArray[ inputArray[1] ]- –

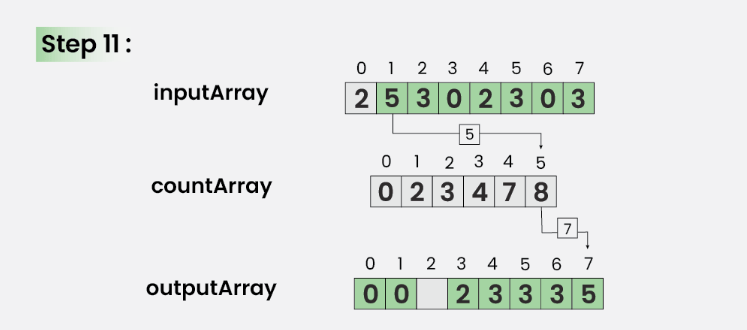
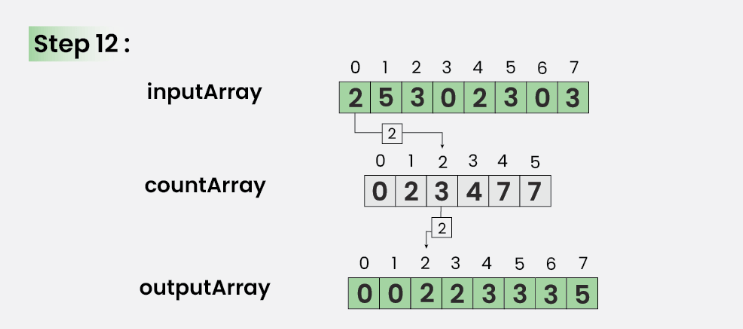
Bước 12: Với i = 0

Cập nhật outArray[ countArray[ inputArray[0] ] – 1] = inputArray[0]
Ngoài ra, cập nhật countArray[ inputArray[0] ] = countArray[ inputArray[0] ]- –

2. Code thuật toán Cycle Sort

function countingSort(arr) {
    // Find the maximum element in the array
    let max = Math.max(...arr);

    // Create a count array and initialize all values to 0
    let count = new Array(max + 1).fill(0);

    // Store the count of each element
    for (let i = 0; i < arr.length; i++) {
        count[arr[i]]++;
    }

    // Store the cumulative count
    for (let i = 1; i <= max; i++) {
        count[i] += count[i - 1];
    }

    // Find the index of each element of the original array in the count array, and
    // place the elements in output array
    let output = new Array(arr.length);
    for (let i = arr.length - 1; i >= 0; i--) {
        output[count[arr[i]] - 1] = arr[i];
        count[arr[i]]--;
    }

    // Copy the sorted elements into original array
    for (let i = 0; i < arr.length; i++) {
        arr[i] = output[i];
    }
}

// Example usage:
let arr = [4, 2, 2, 8, 3, 3, 1];
console.log("Original array:", arr);
countingSort(arr);
console.log("Sorted array:", arr);

3. Phân tích độ phức tạp của thuật toán Cycle Sort

• Độ phức tạp về thời gian : O(N+M), trong đó N và M lần lượt là kích thước của inputArray[] và countArray[] .
  • Trường hợp xấu nhất: O(N+M).
  • Trường hợp trung bình: O(N+M).
  • Trường hợp tốt nhất: O(N+M).
• Không gian phụ trợ: O(N+M), trong đó N và M lần lượt là không gian được lấy bởi outArray[] và countArray[] .

4. Ưu và nhược điểm của Cycle Sort

4.1 Ưu điểm

• Sắp xếp đếm thường hoạt động nhanh hơn tất cả các thuật toán sắp xếp dựa trên so sánh, chẳng hạn như sắp xếp hợp nhất và sắp xếp nhanh, nếu phạm vi đầu vào theo thứ tự số lượng đầu vào.
• Sắp xếp đếm rất dễ mã hóa
• Đếm sắp xếp là một thuật toán ổn định .

4.2 Nhược điểm

• Tính năng sắp xếp không hoạt động trên các giá trị thập phân.
• Việc sắp xếp đếm sẽ không hiệu quả nếu phạm vi giá trị được sắp xếp rất lớn.
• Sắp xếp đếm không phải là thuật toán sắp xếp tại chỗ . Nó sử dụng thêm không gian để sắp xếp các phần tử mảng.

5. Ứng dụng vào thực tế

Counting Sort được sử dụng trong các tình huống mà các phần tử có thể được ánh xạ tới số nguyên trong một phạm vi giới hạn. Ví dụ, nó có thể được sử dụng để sắp xếp các ký tự trong một chuỗi hoặc các số nguyên nhỏ trong các ứng dụng cụ thể.

6. Kết luận

Counting Sort là một thuật toán sắp xếp không so sánh, cực kỳ hiệu quả khi xử lý các mảng có giá trị phần tử nằm trong phạm vi nhỏ và hữu hạn. Với khả năng sắp xếp nhanh chóng và ổn định, nó là một lựa chọn lý tưởng cho các bài toán cụ thể, đặc biệt khi yêu cầu về hiệu suất cao. Tuy nhiên, khi phạm vi giá trị của phần tử quá lớn, Counting Sort có thể trở nên không hiệu quả do yêu cầu bộ nhớ lớn.

7. Tài liệu tham khảo

Để hiểu hơn về thuật toán Cycle Sort bạn có thể truy cập vào: https://www.geeksforgeeks.org/counting-sort/