Thuật toán Fibonacci là một trong những khái niệm nổi tiếng nhất trong khoa học máy tính và toán học. Trong bài viết này, chúng ta sẽ tìm hiểu chi tiết về cách đơn giản nhất để triển khai 1 thuật toán tiêu biểu: tìm số Fibonacci, ứng dụng của nó, và các cách tối ưu khi triển khai.
1. Fibonacci là gì?
Dãy Fibonacci là một dãy số được xác định như sau:
- Số đầu tiên là 0.
- Số thứ hai là 1.
- Mỗi số tiếp theo là tổng hai số trước đó.
Công thức tổng quát: F(n)=F(n−1)+F(n−2)F(n) = F(n-1) + F(n-2)
với F(0)=0F(0) = 0 và F(1)=1F(1) = 1.
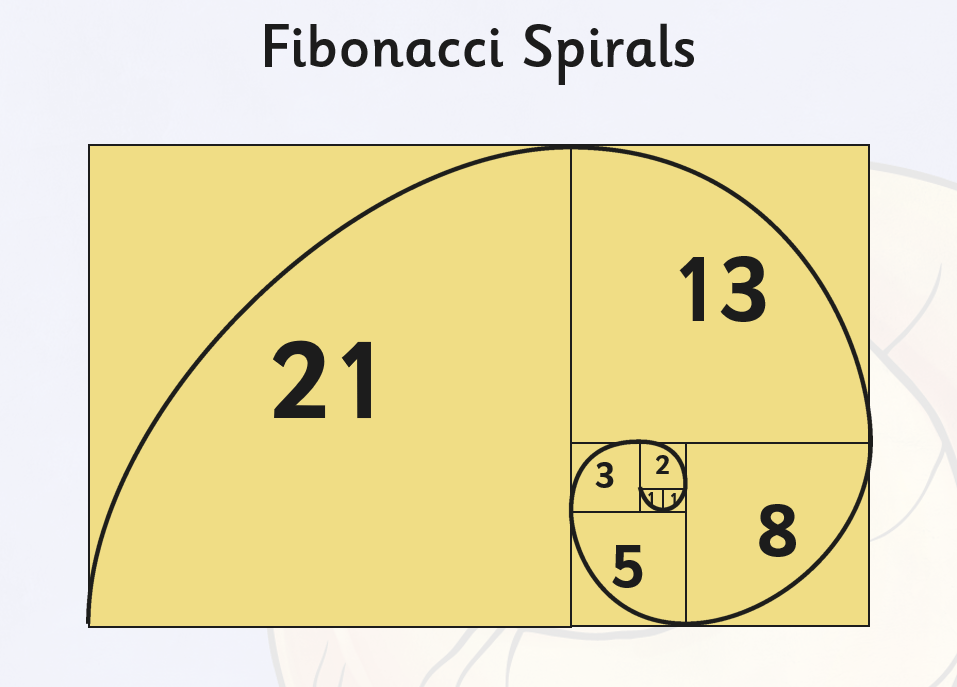
Ví dụ: 0,1,1,2,3,5,8,13,21,34,…0, 1, 1, 2, 3, 5, 8, 13, 21, 34, \dots
2. Ứng dụng của Fibonacci
Dãy Fibonacci xuất hiện trong nhiều lĩnh vực như:
- Toán học: Nghiên cứu tính chất của dãy Fibonacci trong lý thuyết số.
- Khoa học máy tính: Để thiết kế các thuật toán hiệu quả.
- Nghệ thuật: Fibonacci góp phần tạo ra tỷ lệ vàng, một khái niệm được ưa chuộng trong nghệ thuật và thiết kế.
3. Các cách triển khai thuật toán Fibonacci
a) Cách dùng đệ quy
Mã giản đơn bằng Python:
# Triển khai Fibonacci bằng đệ quy
def fibonacci(n):
if n <= 1:
return n
return fibonacci(n-1) + fibonacci(n-2)
print(fibonacci(10)) # Kết quả: 55
Điểm yếu:
- Tốn nhiều tài nguyên do các lời gọi lại (overlapping subproblems).
b) Cách dùng vòng lặp
Phương pháp này hiệu quả hơn:
# Triển khai Fibonacci bằng vòng lặp
def fibonacci_iterative(n):
a, b = 0, 1
for _ in range(n):
a, b = b, a + b
return a
print(fibonacci_iterative(10)) # Kết quả: 55
Điểm mạnh:
- Giảm tính phức tạp tính toán.
c) Dùng quy hoạch động
Quy hoạch động giúp lưu trữ kết quả trung gian để tối ưu hiệu suất.
# Triển khai Fibonacci bằng quy hoạch động
def fibonacci_dp(n):
dp = [0] * (n + 1)
dp[1] = 1
for i in range(2, n + 1):
dp[i] = dp[i-1] + dp[i-2]
return dp[n]
print(fibonacci_dp(10)) # Kết quả: 55
Điểm mạnh:
- Tối ưu về bộ nhớ và tốc độ.
d) Dùng công thức truyền tháng
Công thức truyền tháng dựa trên ma trận:
import numpy as np
def fibonacci_matrix(n):
F = np.matrix([[1, 1], [1, 0]])
return (F**(n-1))[0, 0]
print(fibonacci_matrix(10)) # Kết quả: 55
4. So sánh các cách triển khai
| Phương pháp | Tính phức tạp thời gian | Tính phức tạp không gian |
|---|---|---|
| Đệ quy | O(2^n) | O(n) |
| Vòng lặp | O(n) | O(1) |
| Quy hoạch động | O(n) | O(n) |
| Công thức truyền tháng | O(\log n) | O(1) |



