Big O Notation – O lớn & độ phức tạp của thuật toán

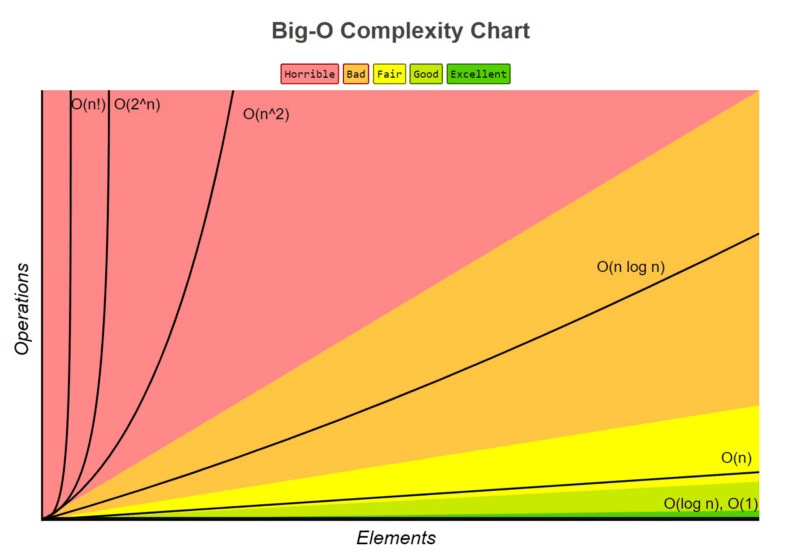
Khái niệm Big O Notation đã được đưa ra để định nghĩa, đo lường tính hiệu quả của một thuật toán. Nó dựa vào số bước cần thực hiện cho một tác vụ nào đó để đo lường tính hiệu quả của thuật toán đó.

Thuật toán là gì?

Đó chính là một chuỗi các bước tính toán được định nghĩa rõ ràng để giải quyết một vấn đề. Nó nhận vào một tập các giá trị đầu vào và trả về một tập các giá trị đầu ra và thường được biểu diễn bằng mã nguồn, mã giả hoặc lưu đồ giải thuật.

Các tính chất cần có của một thuật toán:

• Tính đúng đắn (cần thiết): kết quả trả về phản ánh đúng mong muốn của thông tin nhận vào
• Tính hiệu quả (quan trọng): độ tin cậy, tốc độ xử lý, tài nguyên sử dụng

Big O Notation

Trong toán học, ký hiệu O lớn dùng để chỉ hành vi giới hạn của một hàm số khi đối số tiến đến một giá trị nhất định hoặc vô cùng. Đối với lĩnh vực khoa học máy tính, nó còn dùng để mô tả hành vi thuật toán (ví dụ, về mặt thời gian tính toán hoặc lượng bộ nhớ cần dùng) khi kích thước dữ liệu thay đổi.

– Wikipedia –

Ký hiệu Big-O mô tả các hàm theo tốc độ tăng của chúng: các hàm khác nhau có cùng tốc độ tăng có thể được mô tả bởi cùng một ký hiệu. Một số hàm phổ biến thường gặp như:

• O(1): Độ phức tạp hằng số
• O(log n): Độ phức tạp logarit
• O(n): Độ phức tạp tuyến tính
• O(n²): Độ phức tạp đa thức
• O(aⁿ): Độ phức tạp hàm mũ mũ

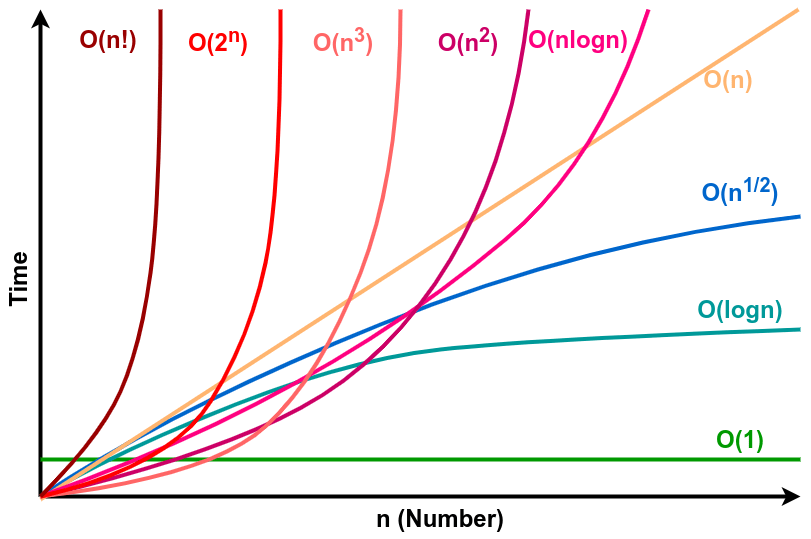
Một số độ phức tạp thông dụng

Big O mô tả cho độ phức tạp của thuật toán

Gọi n là độ lớn đầu vào. Tùy thuộc từng bài toán mà n có thể nhận những giá trị khác nhau. Chẳng hạn, bài toán tính giai thừa thì n chính là số cần tính giai thừa. Trong các phép tính đối với ma trận thì n là số hàng hoặc cột của ma trận.

Độ phức tạp của bài toán phụ thuộc vào n. Ở đây ta không chỉ đặc trưng độ phức tạp bởi số lượng phép tính, mà dùng một đại lượng tổng quát là tài nguyên cần dùng R(n). Đó có thể là số lượng phép tính (có thể tính cả số lần truy nhập bộ nhớ, hoặc ghi vào bộ nhớ); nhưng cũng có thể là thời gian thực hiện chương trình (độ phức tạp về thời gian) hoặc dung lượng bộ nhớ cần phải cấp để chạy chương trình (độ phức tạp về không gian).

Xét quan hệ giữa tài nguyên và độ lớn đầu vào, nếu như tìm được hằng số C > 0, C không phụ thuộc vào n, sao cho với n đủ lớn, các hàm R(n), g(n) đều dương và R(n) ≤ C.g(n) thì ta nói thuật toán có độ phức tạp cỡ O(g(n)).

Phân tích thời gian chạy của thuật toán

Có 2 cách để phân tích thời gian chạy của 1 thuật toán:

• Phương pháp thực nghiệm
  • Đo thời gian chạy thực, vẽ đồ thị, …
  • Có kịch bản tiến hành thực nghiệm
  • Cần cài đặt thuật toán (khó, lâu)
  • Đôi khi không thể chạy hết các bộ dữ liệu
  • Để so sánh các thuật toán, phải sử dụng cùng môi trường (phần cứng & phần mềm)
  • Phù hợp cho dự đoán
• Ứng dụng toán học
  • Ước lượng số phép toán là hàm của độ lớn dữ liệu đầu vào
  • Thông thường thông qua sử dụng mã giả
  • Xét tất cả các bộ dữ liệu đầu vào
  • Không phụ thuộc môi trường tính toán
  • Phù hợp cho cả dự đoán và giải thích
  • Thường được sử dụng để đánh giá

Khi phân tích thuật toán, chúng ta thường xét lần lượt các trường hợp như:

1. Xấu nhất (thông thường): Thời gian chạy lớn nhất của thuật toán trên tất cả các dữ liệu có cùng độ lớn
2. Trung bình (đôi khi): Thời gian chạy trung bình của thuật toán trên tất cả các dữ liệu có cùng độ lớn
3. Tốt nhất (hiếm): Thời gian chạy ít nhất của thuật toán trên tất cả các dữ liệu có cùng độ lớn

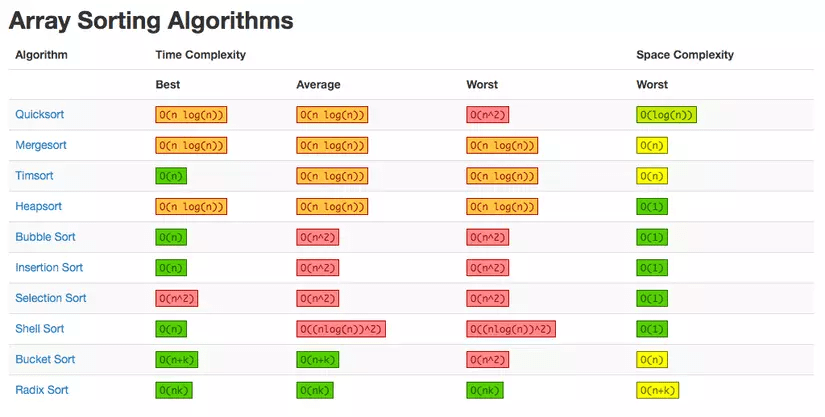
Độ phức tạp của các thuật toán sắp xếp trong 3 trường hợp

Từ mỗi phương pháp xét, chúng ta sẽ rút ra một kết luận về độ phức tạp của thuật toán

Cách tính độ phức tạp của thuật toán bằng phân tích toán học

Bước 1: Đánh giá thời gian chạy của thuật toán T(n) = số lượng phép toán sơ cấp cần thực hiện (số học, logic, so sánh)

Bước 2: Xác định độ tăng của hàm T(n) và bậc tăng trưởng dựa theo tỉ lệ tăng trưởng.

Bước 3: Tìm tiệm cận trên chặt (O lớn) của hàm T(n)

Ví dụ:

1 for (i = 0; i < n; i++)
2   for (j = 0; j < n; j++)
3.    if (i == j)
4.      a[i][j] = 1;
5.    else
6.      a[i][j] = 0;

T₄ = O(1)
T₆ = O(1)
T₃ = O(1)
=> T₃₄₅₆ = O(1)
T₂ = O(n)
=> T₂₃₄₅₆ = O(n) x O(1) = O(n)
T₁ = O(n)
=> T₁₂₃₄₅₆ = O(n) x O(n) = O(n²)

Vậy độ phức tạp của đoạn chương trình bên trên là O(n²).

Tóm lại, Big-O là một lí thuyết được dùng trong toán học, giúp biểu diễn giới hạn tiệm cận của một hàm số. Và trong lĩnh vực khoa học máy tính, khái niệm Big-O được dùng để mô tả cho độ phức tạp tương đối của thuật toán. Một thuật toán có tối ưu hay không sẽ được đánh giá tính hiệu quả thông qua Big-O. Hi vọng bài viết ngắn bên trên sẽ giúp bạn tổng quát hóa về Big-O cũng như biết cách tính toán hàm O lớn. Nếu có bất kì đóng góp nào vui lòng để lại ý kiến bên dưới. Xin chân thành cảm ơn