Cycle Sort là một thuật toán sắp xếp tương đối ít được biết đến, nhưng rất hiệu quả trong các trường hợp yêu cầu số lần ghi (writes) vào mảng là ít nhất có thể. Được phát triển bởi Donald Knuth, Cycle Sort hoạt động tốt trên các mảng có kích thước nhỏ hoặc trung bình và đặc biệt hữu ích trong các bài toán mà chi phí của mỗi lần ghi là đắt đỏ, chẳng hạn như trên bộ nhớ flash.
1. Cách hoạt động của thuật toán Cycle Sort
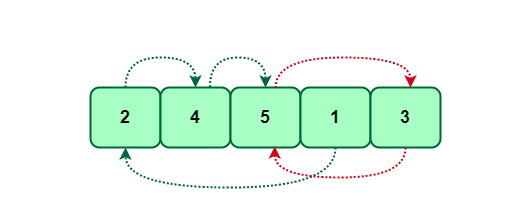
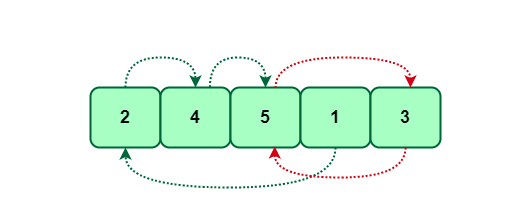
Tương tự như bài viết trước ta sẽ cho 1 ví dụ mảng: arr[] = [2, 4, 5, 1, 3]
Bước 1: Bắt đầu với phần tử đầu tiên (start = 0):
- Phần tử đầu tiên:
2 - Tìm vị trí đúng của 2: Đếm số phần tử nhỏ hơn 2 trong mảng
[2, 4, 5, 1, 3]. Có 1 phần tử nhỏ hơn 2. - Vị trí đúng của 2:
position = 1 - Hoán đổi: Đưa 2 đến vị trí 1. Hoán đổi
arr[1]vớiarr[0]. - Mảng sau hoán đổi:
[4, 2, 5, 1, 3]
Bước 2: Tiếp tục với phần tử ban đầu (start = 0):
- Phần tử tại
arr[0]:4 - Tìm vị trí đúng của 4: Đếm số phần tử nhỏ hơn 4 trong mảng
[4, 2, 5, 1, 3]. Có 3 phần tử nhỏ hơn 4. - Vị trí đúng của 4:
position= 3 - Hoán đổi: Đưa 4 đến vị trí 3. Hoán đổi
arr[3]vớiarr[0]. - Mảng sau hoán đổi:
[1, 2, 5, 4, 3]
Bước 3: Tiếp tục với phần tử ban đầu (start = 0):
- Phần tử tại
arr[0]:1 - Tìm vị trí đúng của 1: Đếm số phần tử nhỏ hơn 1 trong mảng
[1, 2, 5, 4, 3]. Không có phần tử nào nhỏ hơn 1. - Vị trí đúng của 1:
position= 0 - Phần tử 1 đã ở đúng vị trí.
Bước 4: Tiếp tục với phần tử kế tiếp (start = 1):
- Phần tử tại
arr[1]:2 - Tìm vị trí đúng của 2: Đếm số phần tử nhỏ hơn 2 trong mảng
[1, 2, 5, 4, 3]. Không có phần tử nào nhỏ hơn 2 ngoàiarr[0](đã ở đúng vị trí). - Vị trí đúng của 2:
position= 1 - Phần tử 2 đã ở đúng vị trí.
Bước 5: Tiếp tục với phần tử kế tiếp (start = 2):
- Phần tử tại
arr[2]:5 - Tìm vị trí đúng của 5: Đếm số phần tử nhỏ hơn 5 trong mảng
[1, 2, 5, 4, 3]. Có 4 phần tử nhỏ hơn 5. - Vị trí đúng của 5:
position= 4 - Hoán đổi: Đưa 5 đến vị trí 4. Hoán đổi
arr[4]vớiarr[2]. - Mảng sau hoán đổi:
[1, 2, 3, 4, 5]
Bước 6: Tiếp tục với phần tử ban đầu (start = 2):
- Phần tử tại
arr[2]:3 - Tìm vị trí đúng của 3: Đếm số phần tử nhỏ hơn 3 trong mảng
[1, 2, 3, 4, 5]. Có 2 phần tử nhỏ hơn 3. - Vị trí đúng của 3:
position= 2 - Phần tử 3 đã ở đúng vị trí.
Bước 7: Tất cả các phần tử đã được sắp xếp đúng vị trí.
Cuối cùng, ta đã sắp xếp xong mảng arr = [1, 2, 3, 4, 5].
2. Code thuật toán Cycle Sort
function cycleSort(arr) {
let writes = 0;
// Loop through the array to find cycles to rotate.
for (let cycleStart = 0; cycleStart <= arr.length - 2; cycleStart++) {
let item = arr[cycleStart];
// Find the position where we put the element.
let pos = cycleStart;
for (let i = cycleStart + 1; i < arr.length; i++) {
if (arr[i] < item) {
pos++;
}
}
// If the item is already there, this is not a cycle.
if (pos === cycleStart) {
continue;
}
// Otherwise, put the item there or right after any duplicates.
while (item === arr[pos]) {
pos++;
}
[arr[pos], item] = [item, arr[pos]];
writes++;
// Rotate the rest of the cycle.
while (pos !== cycleStart) {
pos = cycleStart;
for (let i = cycleStart + 1; i < arr.length; i++) {
if (arr[i] < item) {
pos++;
}
}
while (item === arr[pos]) {
pos++;
}
[arr[pos], item] = [item, arr[pos]];
writes++;
}
}
return writes;
}
// Example usage:
let arr = [2, 4, 5, 1, 3];
console.log("Original array:", arr);
cycleSort(arr);
console.log("Sorted array:", arr);3. Phân tích độ phức tạp của thuật toán Cycle Sort
- Trường hợp xấu nhất: O(n 2 )
- Trường hợp trung bình: O(n 2 )
- Trường hợp tốt nhất: O(n 2 )
Không gian phụ trợ: O(1)
- Độ phức tạp về không gian là không đổi vì thuật toán này được áp dụng nên nó không sử dụng thêm bất kỳ bộ nhớ nào để sắp xếp.
4. Ưu và nhược điểm của Cycle Sort
4.1 Ưu điểm
- Không cần lưu trữ bổ sung.
- thuật toán sắp xếp tại chỗ.
- Số lần ghi tối thiểu vào bộ nhớ
- Sắp xếp theo chu kỳ rất hữu ích khi mảng được lưu trữ trong EEPROM hoặc FLASH.
4.2 Nhược điểm
- Nó không được sử dụng chủ yếu.
- Nó có độ phức tạp về thời gian cao hơn o(n^2)
- Thuật toán sắp xếp không ổn định.
5. Ứng dụng vào thực tế
- Thuật toán sắp xếp này phù hợp nhất cho các tình huống mà hoạt động ghi hoặc trao đổi bộ nhớ tốn kém.
- Hữu ích cho các vấn đề phức tạp.
6. Kết luận
Cycle Sort là một thuật toán sắp xếp ít được biết đến nhưng rất hiệu quả trong một số trường hợp đặc biệt. Với khả năng tối thiểu số lần ghi vào mảng, nó là một lựa chọn tuyệt vời cho các hệ thống lưu trữ mà mỗi lần ghi có chi phí cao. Mặc dù độ phức tạp thời gian của nó không phải là ưu việt, nhưng trong những tình huống cụ thể, Cycle Sort vẫn có thể là sự lựa chọn tốt nhất.
7. Tài liệu tham khảo
Để hiểu hơn về thuật toán Cycle Sort bạn có thể truy cập vào: https://www.geeksforgeeks.org/cycle-sort/