Radix Sort: Hiểu về thuật toán sắp xếp theo Cơ Số

Radix Sort là một thuật toán sắp xếp không so sánh được sử dụng để sắp xếp các số nguyên. Nó hoạt động dựa trên việc sắp xếp từng chữ số của các số nguyên theo thứ tự từ bé đến lớn hoặc từ lớn đến bé. Thuật toán này dựa trên một chiến lược phân chia, sắp xếp và kết hợp để đạt được kết quả cuối cùng.

1. Cách hoạt động của Radix Sort

Đầu tiên ta cho ví dụ mảng như: array[] = [170, 45, 75, 90, 802, 24, 2, 66]

Bước 1: Tìm phần tử lớn nhất trong mảng là 802. Nó có ba chữ số nên chúng ta sẽ lặp ba lần, một lần cho mỗi vị trí quan trọng.

Bước 2: Sắp xếp các phần tử theo chữ số hàng đơn vị (X=0). Chúng tôi sử dụng kỹ thuật sắp xếp ổn định, chẳng hạn như sắp xếp đếm, để sắp xếp các chữ số ở mỗi vị trí quan trọng.

Sắp xếp theo vị trí đơn vị:

• Thực hiện sắp xếp đếm trên mảng dựa trên các chữ số ở vị trí đơn vị.
• Mảng được sắp xếp dựa trên vị trí đơn vị là [170, 90, 802, 2, 24, 45, 75, 66].

Bước 3: Sắp xếp các phần tử theo chữ số hàng chục.

Sắp xếp theo hàng chục:

• Thực hiện sắp xếp đếm trên mảng dựa trên các chữ số hàng chục.
• Mảng được sắp xếp dựa trên vị trí hàng chục là [802, 2, 24, 45, 66, 170, 75, 90].

Bước 4: Sắp xếp các phần tử theo chữ số hàng trăm.

Sắp xếp theo hàng trăm:

• Thực hiện sắp xếp đếm trên mảng dựa trên các chữ số hàng trăm.
• Mảng được sắp xếp dựa trên vị trí hàng trăm là [2, 24, 45, 66, 75, 90, 170, 802].

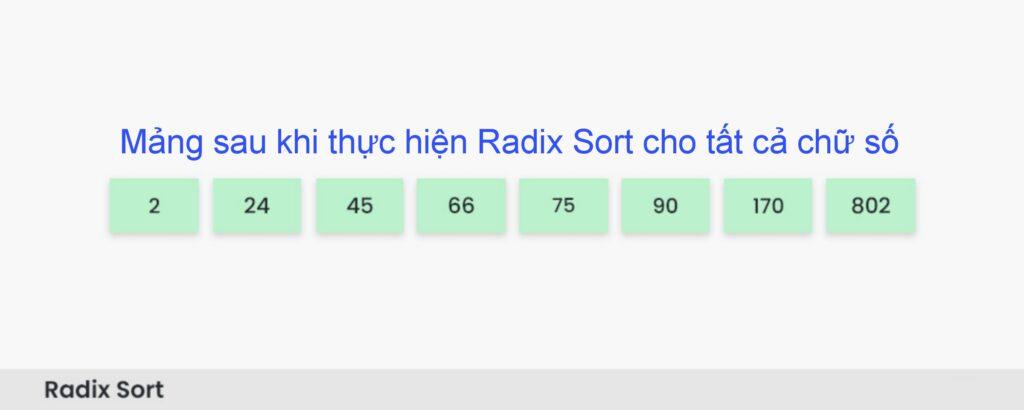
Bước 5: Bây giờ mảng đã được sắp xếp theo thứ tự tăng dần.

Mảng được sắp xếp cuối cùng bằng cách sử dụng sắp xếp cơ số là [2, 24, 45, 66, 75, 90, 170, 802].

2. Code thuật toán Radix Sort

// Hàm để lấy chữ số thứ d trong số nguyên n (tính từ phải sang trái)
function getDigit(num, d) {
    return Math.floor(Math.abs(num) / Math.pow(10, d)) % 10;
}

// Hàm để lấy số lớn nhất trong một mảng
function getMax(arr) {
    let max = 0;
    for (let num of arr) {
        max = Math.max(max, num);
    }
    return max;
}

// Hàm Radix Sort
function radixSort(arr) {
    const maxDigitCount = Math.floor(Math.log10(getMax(arr))) + 1; // Số chữ số lớn nhất trong mảng
    for (let k = 0; k < maxDigitCount; k++) {
        let digitBuckets = Array.from({ length: 10 }, () => []); // Mảng các thùng (buckets) để phân chia các số
        for (let i = 0; i < arr.length; i++) {
            const digit = getDigit(arr[i], k); // Lấy chữ số thứ k của số thứ i
            digitBuckets[digit].push(arr[i]); // Đưa số thứ i vào thùng tương ứng
        }
        arr = [].concat(...digitBuckets); // Kết hợp các thùng lại thành một mảng mới
    }
    return arr;
}

// Sử dụng Radix Sort để sắp xếp một mảng các số nguyên
let arr = [170, 45, 75, 90, 802, 24, 2, 66];
console.log("Mảng trước khi sắp xếp:", arr);
arr = radixSort(arr);
console.log("Mảng sau khi sắp xếp:", arr);

3. Phân tích độ phức tạp của thuật toán

Độ phức tạp về thời gian: 

• Sắp xếp cơ số là một thuật toán sắp xếp số nguyên không so sánh, sắp xếp dữ liệu bằng các khóa số nguyên bằng cách nhóm các khóa theo các chữ số riêng lẻ có cùng vị trí và giá trị quan trọng. Nó có độ phức tạp về thời gian là O(d * (n + b)) , trong đó d là số chữ số, n là số phần tử và b là cơ sở của hệ thống số đang được sử dụng.
• Trong triển khai thực tế, sắp xếp cơ số thường nhanh hơn các thuật toán sắp xếp dựa trên so sánh khác, chẳng hạn như sắp xếp nhanh hoặc sắp xếp hợp nhất, đối với các tập dữ liệu lớn, đặc biệt khi các khóa có nhiều chữ số. Tuy nhiên, độ phức tạp về thời gian của nó tăng tuyến tính theo số chữ số và do đó nó không hiệu quả đối với các tập dữ liệu nhỏ.

Không gian phụ trợ: 

• Sắp xếp cơ số cũng có độ phức tạp về không gian là O(n + b), trong đó n là số phần tử và b là cơ số của hệ thống số. Sự phức tạp về không gian này xuất phát từ nhu cầu tạo các nhóm cho mỗi giá trị chữ số và sao chép các phần tử trở lại mảng ban đầu sau khi mỗi chữ số đã được sắp xếp.

4. Ưu và nhược điểm của thuật toán

4.1 Ưu điểm của thuật toán

• Hiệu suất tốt với các số nguyên dương: Radix Sort hoạt động tốt với các số nguyên dương và không cần phải so sánh giữa các phần tử.
• Dễ dàng cài đặt: Thuật toán này có thể dễ dàng cài đặt và hiểu.
• Ổn định: Nếu sử dụng một thuật toán sắp xếp ổn định trong mỗi bước, Radix Sort sẽ cũng là một thuật toán ổn định.

4.2 Nhược điểm

• Chỉ hoạt động với số nguyên không âm: Radix Sort không thích hợp cho các số nguyên âm nếu không có xử lý đặc biệt.
• Không hiệu quả với các số lớn có phạm vi lớn: Nếu phạm vi của số lớn, Radix Sort có thể trở nên không hiệu quả vì số lượng thùng cần phải tạo ra có thể rất lớn.
• Không phù hợp với các tập dữ liệu không có phân phối đồng đều: Nếu dữ liệu không phân phối đều, các thùng có thể có kích thước lớn khác nhau, làm giảm hiệu suất của thuật toán.

5. Kết luận

Radix Sort là một thuật toán sắp xếp mạnh mẽ cho các số nguyên không âm. Dựa vào cơ chế phân chia và sắp xếp từng chữ số, nó đạt được hiệu suất tốt trong một số trường hợp nhất định. Tuy nhiên, cần phải xem xét kỹ lưỡng các điều kiện đặc biệt của dữ liệu trước khi quyết định sử dụng Radix Sort cho một bài toán cụ thể.

Reference: https://www.geeksforgeeks.org/radix-sort/