Trong thế giới của lập trình và khoa học máy tính, việc sắp xếp dữ liệu là một nhiệm vụ quan trọng. Có nhiều phương pháp để thực hiện công việc này, và mỗi phương pháp đều có những ưu và nhược điểm riêng của nó. Trong số các phương pháp đó, “Insertion Sort” là một trong những cách đơn giản nhất và dễ hiểu nhất.
1. Thuật toán Insertion Sort là gì?
Insertion Sort là một thuật toán sắp xếp đơn giản nhưng mạnh mẽ. Ý tưởng cơ bản của nó là chia mảng thành hai phần: một phần được sắp xếp và một phần chưa được sắp xếp. Thuật toán sẽ duyệt qua từng phần tử trong phần chưa được sắp xếp, chèn nó vào đúng vị trí trong phần đã được sắp xếp.
2. Cách hoạt động của Insertion Sort
Như các bài trước ta tiếp tục cho ví dụ mảng: arr[] = [23, 1, 10, 5, 2]
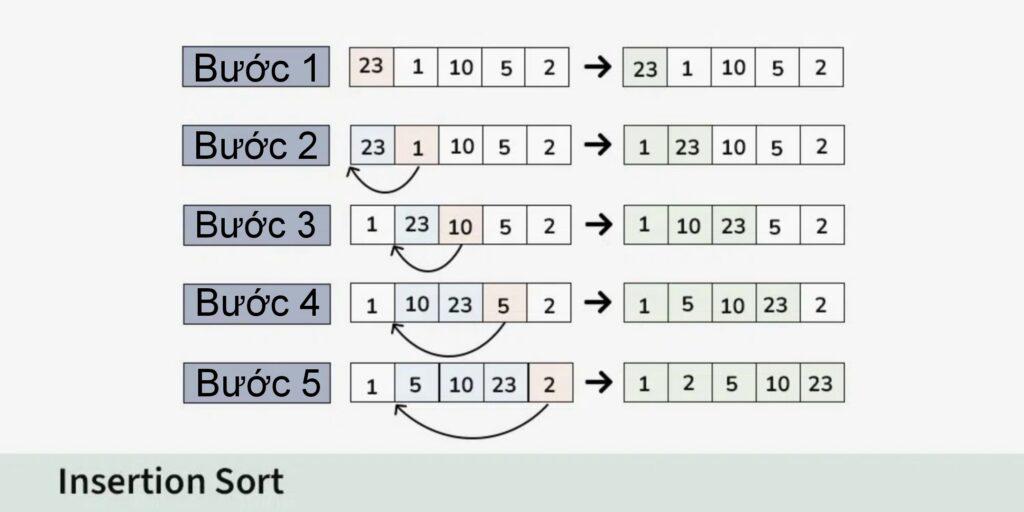
Bước 1:
- Phần tử hiện tại là 23
- Phần tử đầu tiên trong mảng được coi là đã được sắp xếp.
- Phần được sắp xếp cho đến index 0 là: [23]
Bước 2:
- So sánh 1 với 23 (phần tử hiện tại với phần được sắp xếp).
- Vì 1 nhỏ hơn nên chèn 1 trước 23 .
- Phần được sắp xếp cho đến index 1 là: [1, 23]
Bước 3:
- So sánh 10 với 1 và 23 (phần tử hiện tại với phần được sắp xếp).
- Vì 10 lớn hơn 1 và nhỏ hơn 23 nên chèn 10 vào giữa 1 và 23 .
- Phần được sắp xếp cho đến index 2 là: [1, 10, 23]
Bước 4:
- So sánh 5 với 1 , 10 và 23 (phần tử hiện tại với phần được sắp xếp).
- Vì 5 lớn hơn 1 và nhỏ hơn 10 nên chèn 5 vào giữa 1 và 10 .
- Phần được sắp xếp cho đến index 3 là : [1, 5, 10, 23]
Bước 5:
- So sánh 2 với 1, 5, 10 và 23 (phần tử hiện tại với phần được sắp xếp).
- Vì 2 lớn hơn 1 và nhỏ hơn 5 nên chèn 2 vào giữa 1 và 5.
- Phần được sắp xếp cho đến index 4 là: [1, 2, 5, 10, 23]
Bước cuối:
- Mảng được sắp xếp là: [1, 2, 5, 10, 23]
3. Code thuật toán
function insertionSort(arr) {
const n = arr.length;
for (let i = 1; i < n; i++) {
let current = arr[i];
let j = i - 1;
while (j >= 0 && arr[j] > current) {
arr[j + 1] = arr[j];
j--;
}
arr[j + 1] = current;
}
return arr;
}
// Sử dụng hàm insertionSort để sắp xếp một mảng
const array = [5, 3, 8, 2, 1, 4];
console.log("Mảng trước khi sắp xếp:", array);
console.log("Mảng sau khi sắp xếp:", insertionSort(array.slice()));
// Lưu ý: slice() được sử dụng để tạo ra một bản sao của mảng để tránh ảnh hưởng đến mảng gốc.
4. Phân tích độ phức tạp của thuật toán Insertion Sort
- Trường hợp tốt nhất: O(n) , Nếu danh sách đã được sắp xếp, trong đó n là số phần tử trong danh sách.
- Trường hợp trung bình: O(n 2 ) , Nếu danh sách được sắp xếp ngẫu nhiên
- Trường hợp xấu nhất: O(n 2 ) , Nếu danh sách theo thứ tự ngược lại
Độ phức tạp về không gian của sắp xếp chèn
- Không gian phụ trợ: O(1), Sắp xếp chèn yêu cầu O(1) không gian bổ sung, khiến nó trở thành thuật toán sắp xếp tiết kiệm không gian.
5. Ưu và nhược điểm
5.1 Ưu điểm
- Đơn giản và dễ thực hiện.
- Thuật toán sắp xếp ổn định.
- Hiệu quả cho danh sách nhỏ và danh sách gần như được sắp xếp.
- Không gian hiệu quả.
5.2 Nhược điểm
- Không hiệu quả cho danh sách lớn.
- Không hiệu quả bằng các thuật toán sắp xếp khác (ví dụ: sắp xếp hợp nhất, sắp xếp nhanh) trong hầu hết các trường hợp.
6. Ứng dụng thực tế
Mặc dù Insertion Sort không phải là thuật toán nhanh nhất, nhưng nó vẫn có các ứng dụng trong thực tế. Cụ thể, khi chúng ta có một số lượng nhỏ dữ liệu hoặc dữ liệu gần như đã được sắp xếp, Insertion Sort có thể là một lựa chọn tốt. Nó cũng được sử dụng trong việc sắp xếp dữ liệu trên các cơ sở dữ liệu nhỏ hoặc khi viết mã cho các thiết bị có tài nguyên hạn chế.
Trong tổng quát, việc hiểu và biết cách triển khai thuật toán Insertion Sort không chỉ giúp chúng ta nắm bắt được cách thức hoạt động của nó mà còn giúp chúng ta có cái nhìn sâu hơn về các thuật toán sắp xếp khác.
7. Kết luận
Insertion Sort có thể là một công cụ hữu ích trong hộp công cụ của bất kỳ lập trình viên nào. Tính đơn giản và dễ hiểu của nó làm cho nó trở thành một lựa chọn phổ biến trong nhiều tình huống. Tuy nhiên, cần lưu ý rằng nó không phải là thuật toán tốt nhất cho tất cả các trường hợp, và việc lựa chọn thuật toán phù hợp với bài toán cụ thể là rất quan trọng.
8. Tài liệu
Để hiểu rõ hơn về thuật toán này bạn có thể tới địa chỉ này nhé: https://www.geeksforgeeks.org/insertion-sort/

