Có sáu toán tử bitwise (còn được gọi là bit operators vì chúng hoạt động tại mức độ bit) được sử dụng để thực hiện các phép toán bitwise trong C.
Toán tử & (bitwise AND)
Toán tử & (bitwise AND) trong C lấy hai số làm toán hạng và thực hiện phép AND trên từng bit của hai số. Kết quả của AND là 1 chỉ khi cả hai bit đều là 1.
Ví dụ
#include <stdio.h>
int main()
{
// a = 5(00000101), b = 9(00001001)
unsigned char a = 5, b = 9;
// The result is 00000001
printf("a&b = %d\n", a & b);
return 0;
}Output:
a&b = 1
Toán tử | (bitwise OR)
Toán tử | (bitwise OR) trong C lấy hai số làm toán hạng và thực hiện phép OR trên từng bit của hai số. Kết quả của OR là 1 nếu bất kỳ một trong hai bit là 1.
Ví dụ
#include <stdio.h>
int main()
{
// a = 5(00000101), b = 9(00001001)
unsigned char a = 5, b = 9;
// The result is 00001101
printf("a|b = %d\n", a | b);
return 0;
}Output:
a|b = 13
Toán ^ (bitwise XOR)
Toán ^ (bitwise XOR) trong C lấy hai số làm toán hạng và thực hiện phép XOR trên từng bit của hai số. Kết quả của XOR là 1 nếu hai bit khác nhau.
Ví dụ
#include <stdio.h>
int main()
{
// a = 5(00000101), b = 9(00001001)
unsigned char a = 5, b = 9;
// The result is 00001100
printf("a^b = %d\n", a ^ b);
return 0;
}Output:
a^b = 12
Toán tử << (left shift)
Toán tử << (left shift) trong C lấy hai số, dịch trái các bit của toán hạng đầu tiên và toán hạng thứ hai quyết định số lượng vị trí cần dịch.
Ví dụ
#include <stdio.h>
int main()
{
// a = 5(00000101), b = 9(00001001)
unsigned char a = 5, b = 9;
// The result is 00010010
printf("b<<1 = %d\n", b << 1);
return 0;
}Output:
b<<1 = 18
Toán tử >> (right shift)
Toán tử >> (right shift) trong C lấy hai số, dịch phải các bit của toán hạng đầu tiên và toán hạng thứ hai quyết định số lượng vị trí cần dịch.
Ví dụ
#include <stdio.h>
int main()
{
// a = 5(00000101), b = 9(00001001)
unsigned char a = 5, b = 9;
// The result is 00000100
printf("b>>1 = %d\n", b >> 1);
return 0;
}Output:
b>>1 = 4
Toán tử ~ (bitwise NOT)
Toán tử ~ (bitwise NOT) trong C lấy một số và đảo ngược tất cả các bit của nó.
Ví dụ
#include <stdio.h>
int main()
{
// a = 5(00000101), b = 9(00001001)
unsigned char a = 5, b = 9;
// The result is 11111010
printf("~a = %d\n", a = ~a);
return 0;
}Output:
~a = 250
Bảng chân trị của các toán tử bitwise trong C
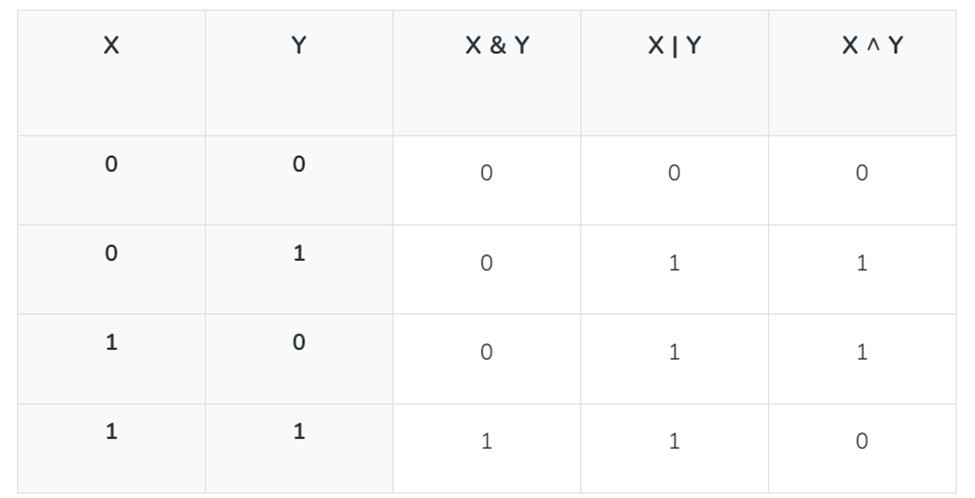
Các toán tử này không có bảng chân trị vì chúng thực hiện các phép dịch nhị phân thay vì các phép toán logic.
Những Sự Thú Vị Về Các Toán Tử Bitwise
1. Các toán tử dịch trái và dịch phải không nên được sử dụng cho các số âm.
Nếu toán hạng thứ hai (quyết định số lần dịch) là một số âm, điều này dẫn đến hành vi không xác định trong C. Ví dụ, kết quả của cả 1 <<- 1 và 1 >> -1 đều không xác định. Ngoài ra, nếu số được dịch nhiều hơn kích thước của số nguyên, hành vi cũng không xác định. Ví dụ, 1 << 33 là không xác định nếu các số nguyên được lưu trữ bằng 32 bit. Một điều khác là KHÔNG có phép dịch nào được thực hiện nếu biểu thức cộng (toán hạng quyết định số lần dịch) là 0.
2. Phép OR bitwise của hai số chỉ là tổng của hai số đó nếu không có carry được liên quan, nếu không, bạn chỉ cần thêm phép AND bitwise của chúng.
Ví dụ, chúng ta có a=5(101) và b=2(010), vì không có carry được liên quan, tổng của chúng chỉ là a|b. Bây giờ, nếu chúng ta thay đổi ‘a’ thành 6, tức là 110 trong hệ nhị phân, tổng của chúng sẽ thay đổi thành a|b + a&b vì có carry được liên quan.
3.Toán tử XOR bitwise là toán tử hữu ích nhất từ góc độ phỏng vấn kỹ thuật.
Nó được sử dụng trong nhiều vấn đề. Một ví dụ đơn giản có thể là “Cho một tập hợp các số trong đó tất cả các phần tử xuất hiện một số lần chẵn ngoại trừ một số, hãy tìm số xuất hiện lẻ.” Vấn đề này có thể được giải quyết một cách hiệu quả bằng cách thực hiện phép XOR cho tất cả các số.
4.Các toán tử bitwise không nên được sử dụng thay thế cho các toán tử logic.
Kết quả của các toán tử logic (&&, || và !) là 0 hoặc 1, nhưng các toán tử bitwise trả về một giá trị số nguyên. Ngoài ra, các toán tử logic xem xét bất kỳ toán hạng không bằng không nào là 1.
5.Toán tử & có thể được sử dụng để nhanh chóng kiểm tra xem một số có là số lẻ hay số chẵn không.
Giá trị của biểu thức (x & 1) sẽ khác không chỉ nếu x là số lẻ, nếu không, giá trị sẽ là không.
6.Toán tử ~ nên được sử dụng cẩn thận.
Kết quả của toán tử ~ trên một số nhỏ có thể là một số lớn nếu kết quả được lưu trữ trong một biến không dấu. Kết quả có thể là một số âm nếu kết quả được lưu trữ trong một biến có dấu (giả sử rằng các số âm được lưu trữ dưới dạng bù hai với bit trái nhất là bit dấu).
Tài liệu tham khảo: https://www.geeksforgeeks.org/bitwise-operators-in-c-cpp/


