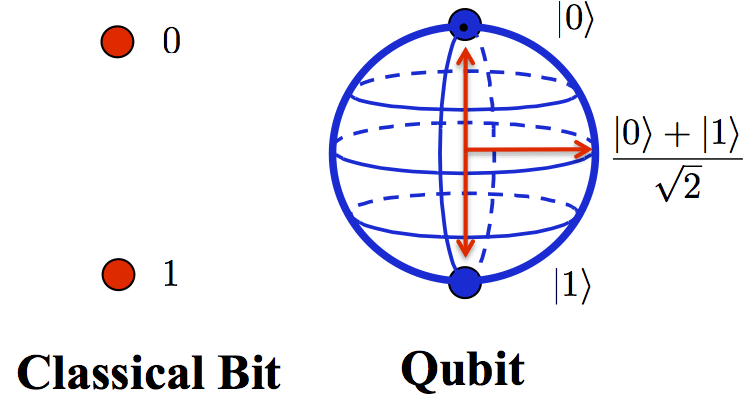
Quantum Gate – Điện toán lượng tử sử dụng các bit lượng tử hoặc qubit có thể biểu thị sự chồng chất của 0 và 1. Điều này cho phép các qubit thực hiện tính toán đồng thời trên tất cả các trạng thái có thể. Tuy nhiên, hành vi này có thể phản trực giác khi so sánh với các bit nhị phân cổ điển. Hình dung cách các hoạt động lượng tử thao túng trạng thái qubit có thể giúp xây dựng trực giác về cách thức hoạt động của thuật toán lượng tử. Trong bài đăng này, chúng ta sẽ xem xét 7 cổng lượng tử qubit đơn phổ biến nhất và cách chúng biến đổi trạng thái qubit trên quả cầu Bloch.
Bài blog được dịch từ blog tiếng anh của thầy Thinh Q. Dinh: https://thinhqdinh.github.io/blog/2023/ep5/
Quả cầu Bloch
Trạng thái của một qubit đơn lẻ có thể được biểu diễn dưới dạng một điểm trên bề mặt của quả cầu Bloch. Các cực tương ứng với trạng thái |0> và |1>. Tất cả các điểm khác thể hiện sự chồng chất của |0> và |1> được xác định bởi hai góc –θ Và ϕ trong tọa độ cầu [ r , θ , ϕ ]
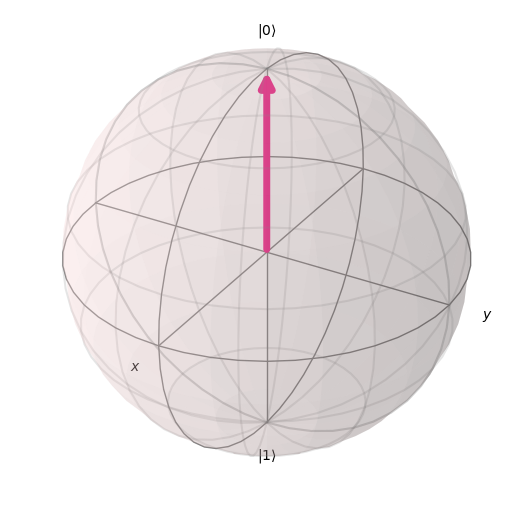
Trực quan hóa trạng thái |0>
import numpy as np
from qiskit.visualization import plot_bloch_vector
# You can use spherical coordinates instead of cartesian.
plot_bloch_vector([1, 0, 0], coord_type='spherical')
Trực quan hóa trạng thái |1>
plot_bloch_vector([1, np.pi, 0], coord_type='spherical')

Cổng Pauli X (NOT)
Cổng Pauli X, còn gọi là cổng NOT, thực hiện đảo bit, biến đổi ∣ 0 > ĐẾN ∣ 1 >và ngược lại. Trên quả cầu Bloch, nó tương ứng với một góc quay 180° quanh trục x.
from qiskit import QuantumCircuit
qc = QuantumCircuit(1)
qc.x(0)
qc.draw('mpl')
from qiskit.visualization import visualize_transition
visualize_transition(qc, trace = True,saveas = "x_gate.gif", fpg = 20, spg = 2)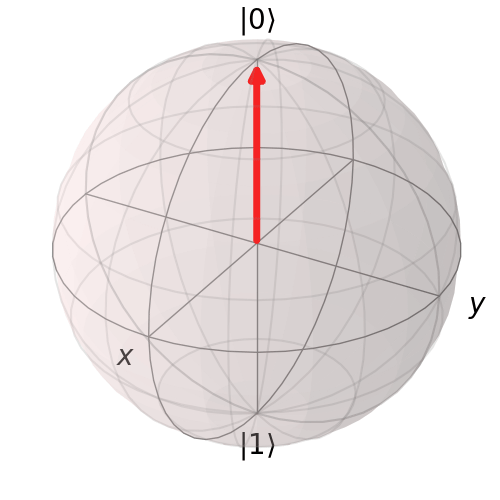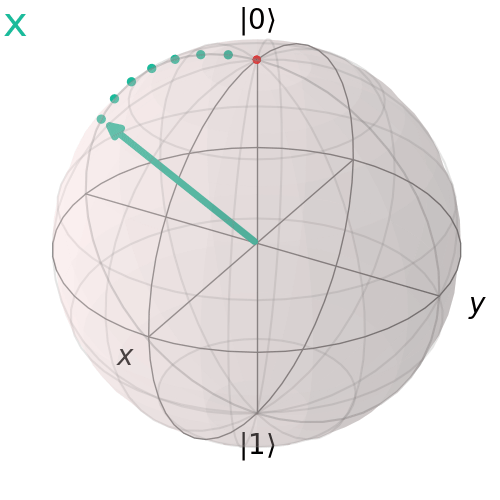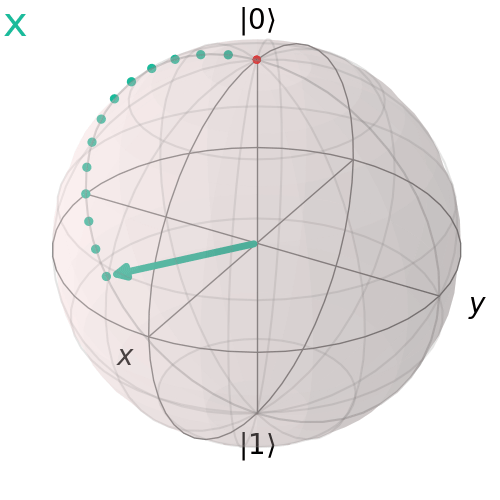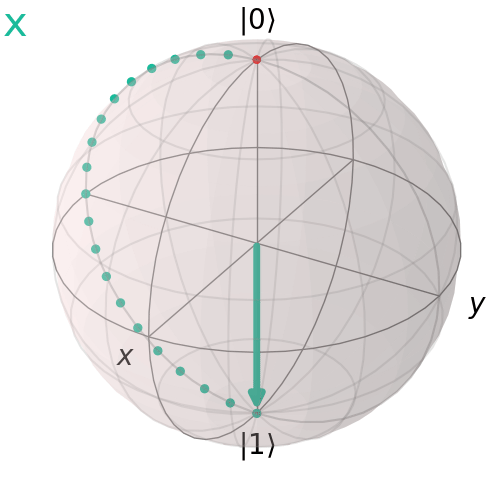
Cổng Pauli Y
Cổng Pauli Y thực hiện đảo bit và đảo pha. Nó xoay trạng thái qubit 180° quanh trục y.
qc = QuantumCircuit(1)
qc.y(0)
qc.draw('mpl')
visualize_transition(qc, trace = True,saveas = "y_gate.gif", fpg = 20, spg = 2)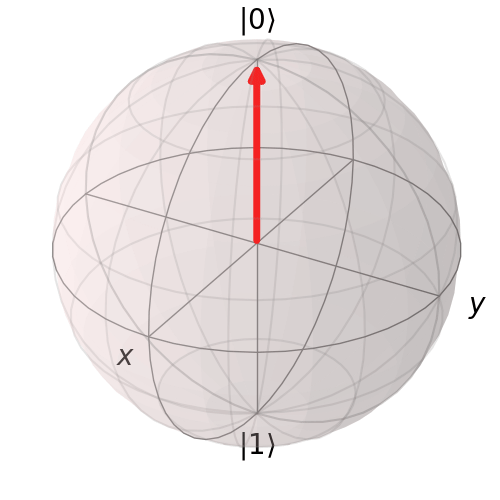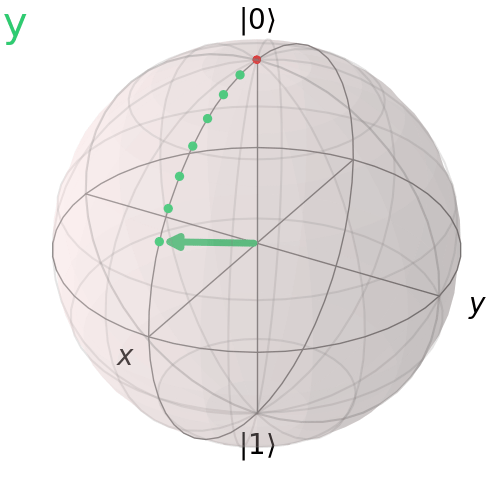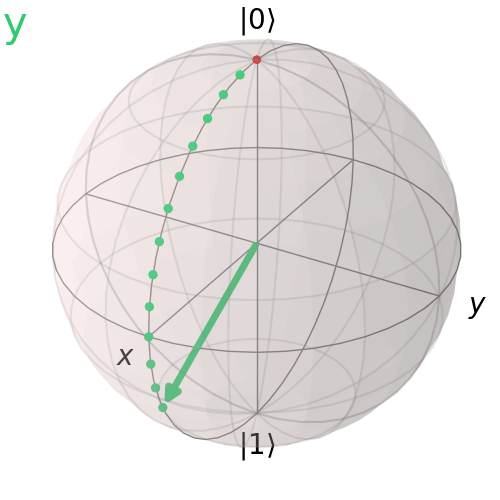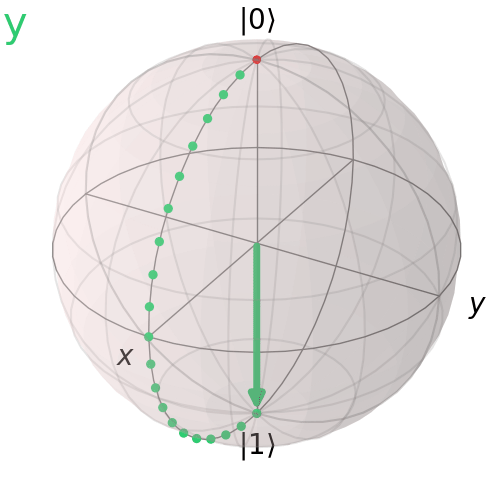
Cổng Pauli Z
Pauli Z tương ứng với góc quay 180° quanh trục z.
qc = QuantumCircuit(1)
qc.h(0)
qc.z(0)
qc.draw('mpl')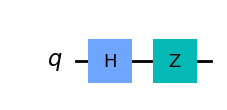
visualize_transition(qc, trace = True,saveas = "z_gate.gif", fpg = 20, spg = 2)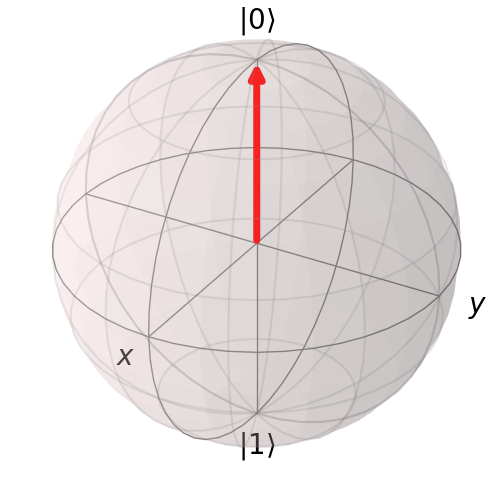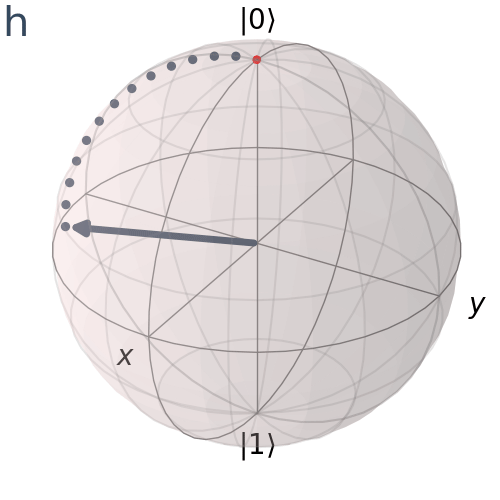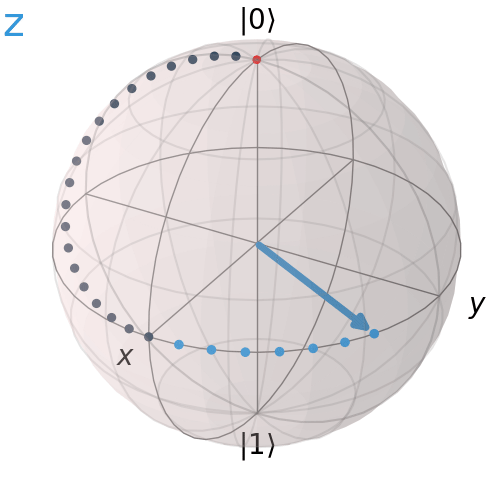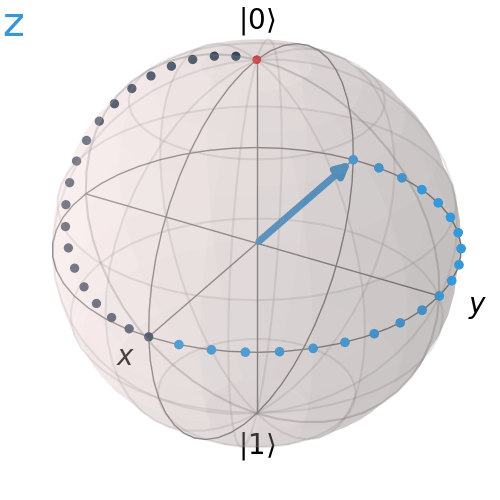
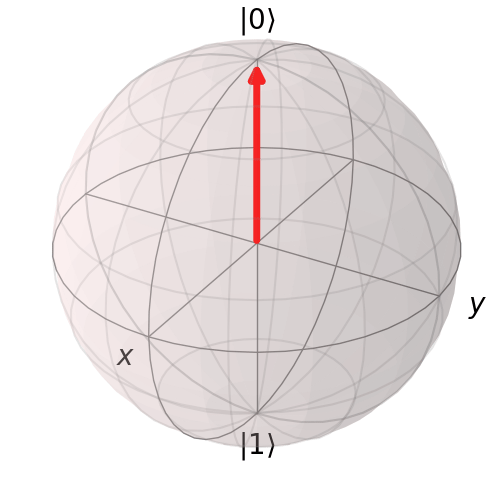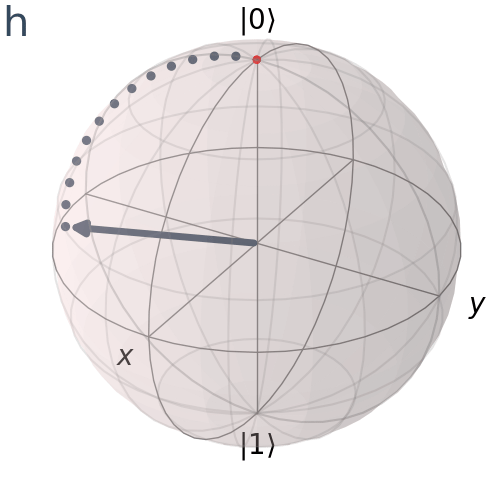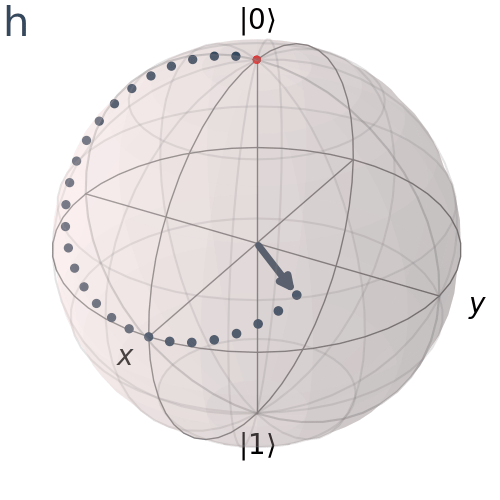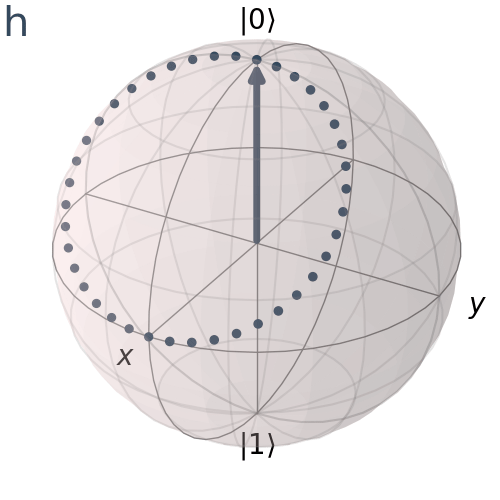
Cổng Hadamard
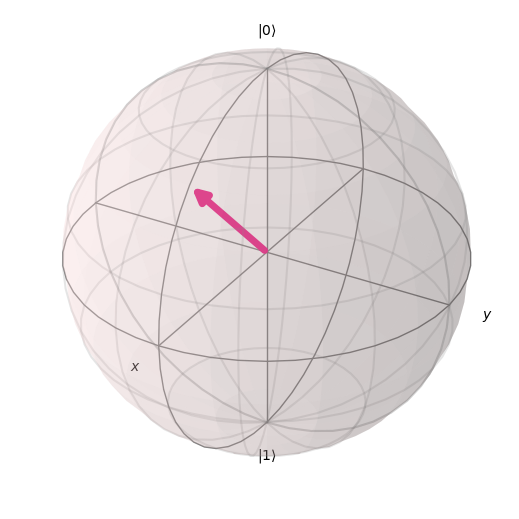
Cổng Hadamard là một thành phần cơ bản trong điện toán lượng tử áp dụng sự chồng chất đồng nhất của các trạng thái vào một qubit. Không giống như các cổng Pauli, quay quanh một trong các trục chính x, y và z, cổng Hadamard quay trạng thái lượng tử của chúng ta bằng pi radian hoặc 180 độ quanh vectơ Bloch [1 0 1] là vectơ chỉ một nửa giữa trục x và trục z
qc = QuantumCircuit(1)
qc.h(0)
qc.draw('mpl')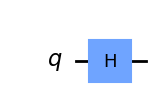
Hình dung trục quay H
plot_bloch_vector([1, np.pi/4, 0], coord_type='spherical')
visualize_transition(qc, trace = True,saveas = "h_gate.gif", fpg = 20, spg = 3)

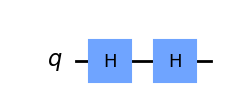
Do đó, áp dụng hai thao tác H liên tiếp, ta quay trở lại vị trí ban đầu
qc = QuantumCircuit(1)
qc.h(0)
qc.h(0)
qc.draw('mpl')
visualize_transition(qc, trace = True,saveas = "2h_gate.gif", fpg = 20, spg = 3)
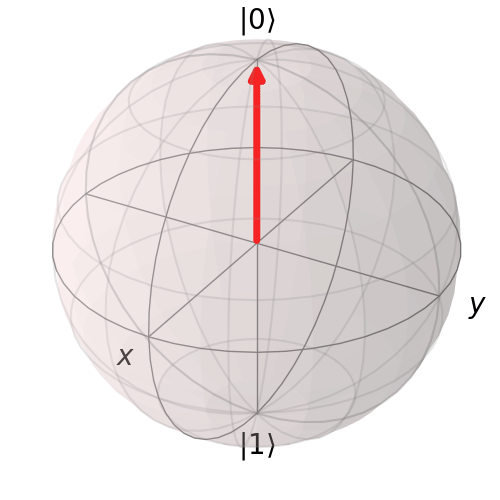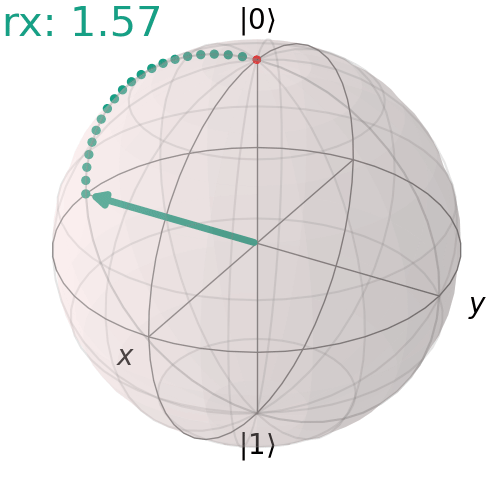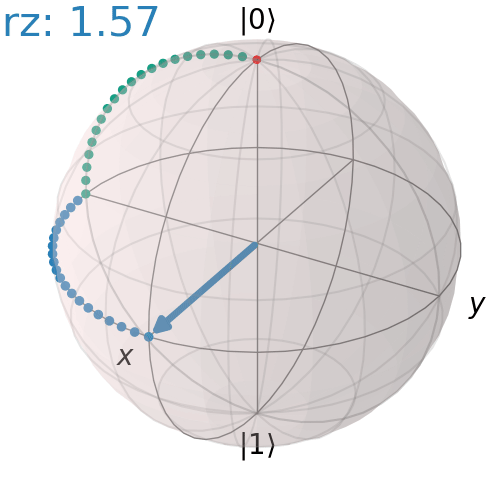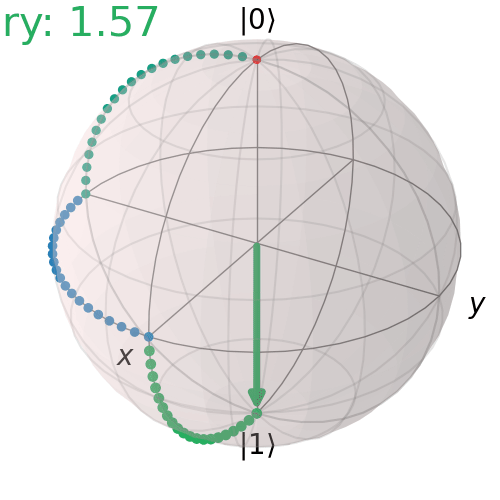
Cổng RX, RY, RZ
Chúng thực hiện các phép quay qubit đơn tùy ý quanh trục X, Y và Z. Góc quay được chỉ định làm tham số.
Cổng RX đơn
Đây là một ví dụ về góc quay 90° quanh trục X.
qc = QuantumCircuit(1)
qc.rx(np.pi/2,0)
qc.draw('mpl')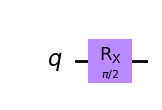
visualize_transition(qc, trace = True,saveas = "rx_gate.gif", fpg = 20, spg = 3)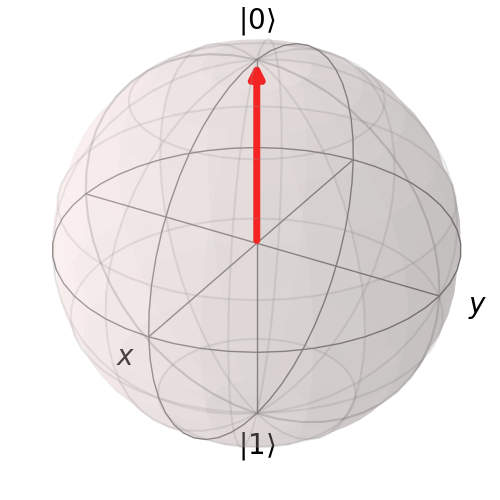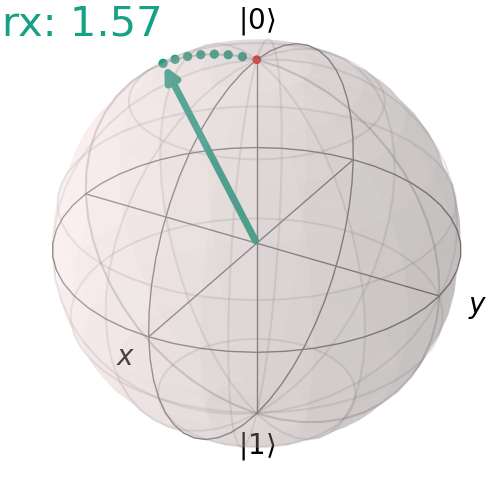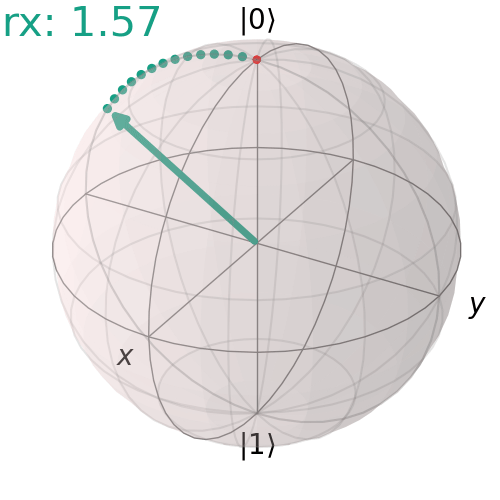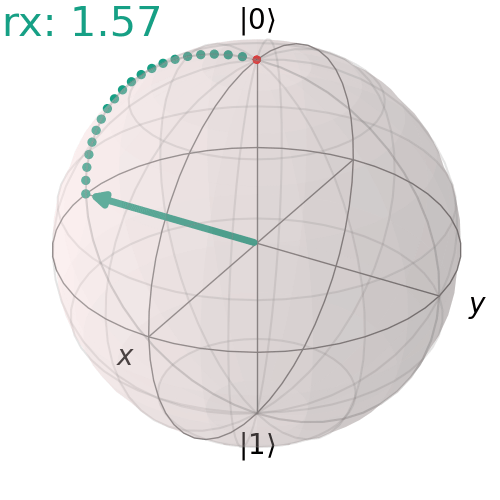
Trình tự các cổng RX, RY, RZ
Dưới đây là ví dụ về xoay 90° quanh trục X, sau đó xoay 90° quanh trục Z, sau đó xoay 90° quanh trục Y
qc = QuantumCircuit(1)
qc.rx(np.pi/2,0)
qc.rz(np.pi/2,0)
qc.ry(np.pi/2,0)
qc.draw('mpl')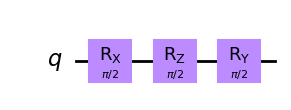
visualize_transition(qc, trace = True,saveas = "3r_gates.gif", fpg = 20, spg = 3)