Bit và xử lý bit trong lập trình giải thuật

Bài viết sẽ được viết dựa trên ngôn ngữ C++

1. Bit và hệ nhị phân:

Bit là đơn vị nhỏ nhất trong hệ thống thông tin kỹ thuật số. Nó chỉ có hai trạng thái, thường được biểu diễn bằng hai giá trị 0 hoặc 1 (false hoặc true) trong hệ nhị phân.

Hệ nhị phân chính là hệ cơ số 2 mà các số hệ nhị phân sẽ được biểu diễn dưới dạng các chữ số 0 và 1.

Trong C++, kiểu int là kiểu số nguyên 32 bit nghĩa là nó có giới hạn từ -2³² đến 2³² – 1. Tương tự là long long là kiểu số nguyên 64 bit.
Ở trong giải thuật c++, có một khái niệm gọi là bitmask, nó là các dãy 0 và 1. Thì cái bit thứ i nó có giá trị là 0 hoặc 1 và nó sẽ tương ứng với 1 ý nghĩa nào đấy. Và với mỗi bitmask ta coi đấy là 1 trạng thái.
- Ví dụ: mình có 1 dãy 5 cái đèn, bit thứ i tương trưng cho trạng thái đèn thứ i bật hoặc tắt, 1 là bật, 0 là tắt.
- Với một dãy bitmask 10101 -> đèn thứ 0 là bật tương tự đèn 4 và 2 cũng bật còn các đèn còn lại thì tắt.
Xử lý bit sẽ giúp chúng ta làm việc với các số nguyên một cách nhanh chóng và có thể vận dụng để làm việc với các bitmask để giải quyết được với một số bài toán trạng thái.

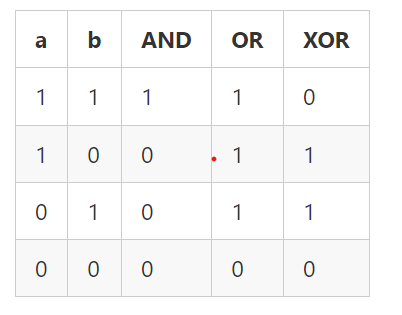
Bảng này là bảng chân trị thể hiện 3 phép AND, OR, XOR 2 bit bất kì

a. Toán tử AND:

b. Toán tử OR:

int a = 5, b =3;
cout << (a|b);
// in ra 7
// 101|11 = 111
// C++

c. Toán tử XOR:

d. Toán tử NOT:

e. Phép dịch trái:

Cú pháp là a << b:
- Nghĩa là dịch tất cả các bit của a sang trái b bit
- Ví dụ: 101 << 2 = 10100

Giải thích:
- 101 = 1*2² + 0*2¹ + 1*2⁰
- 10100 = 1*2⁴ + 0*2³ + 1*2²+ 0*2¹ + 0*2⁰
- So sánh các luỹ thừa của 2 ta sẽ thấy phép dịch bit sang trái tương ứng với phép nhân 2

f. Phép dịch phải:

Kí hiệu là >>
Cú pháp là a >> b:
- Nghĩa là dịch tất cả các bit của a sang phải b bit, nói tắt là cắt mất b bit bên phải của a
- Ví dụ: 101001 >> 3 = 101
Tương ứng với phép chia với 2^b, với mỗi số 0 thêm vào là 1 cơ số 2
Giải thích:
- 101 = 1*2² + 0*2¹ + 1*2⁰
- 10100 = 1*2⁴ + 0*2³ + 1*2²+ 0*2¹ + 0*2⁰
- So sánh các luỹ thừa của 2 ta sẽ thấy phép dịch bit sang phải tương ứng với phép chia 2