Thuật toán Dijkstra là một trong những thuật toán quan trọng và phổ biến nhất trong lĩnh vực khoa học máy tính và mạng. Nó được sử dụng để tìm đường ngắn nhất giữa hai điểm trong một đồ thị, một vấn đề thường gặp trong định tuyến và lập kế hoạch.
1. Giới Thiệu Về Thuật Toán Dijkstra

Edsger W. Dijkstra
Thuật toán Dijkstra được Edsger W. Dijkstra giới thiệu vào năm 1956. Thuật toán này được thiết kế để giải quyết bài toán tìm đường ngắn nhất trong đồ thị có trọng số dương. Điều này có nghĩa là tất cả các cạnh trong đồ thị phải có trọng số không âm.
2. Cách Thuật Toán Dijkstra Hoạt Động
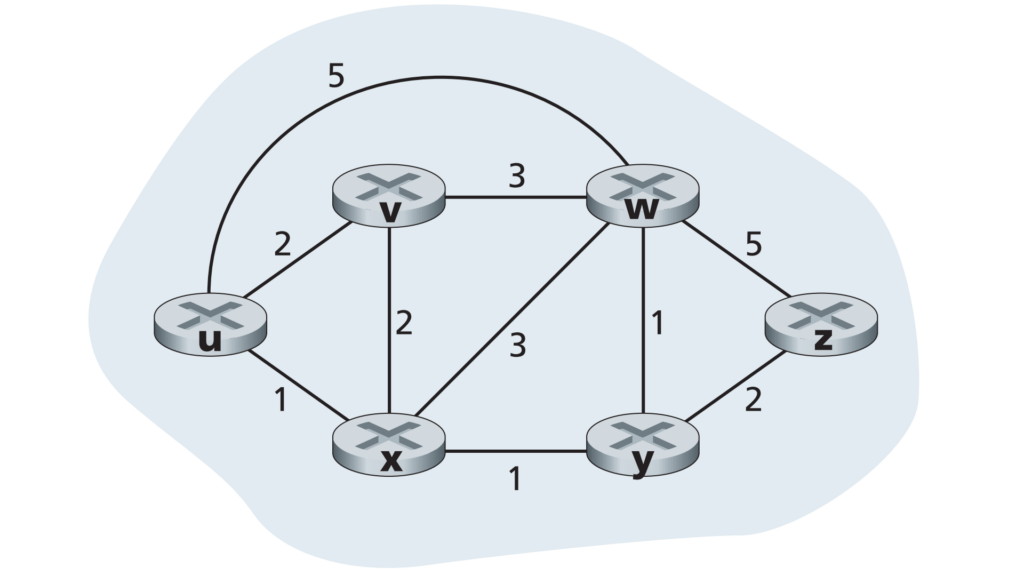
Để hiểu cách hoạt động của thuật toán Dijkstra, hãy xem xét một đồ thị có các đỉnh (điểm) và các cạnh (đường nối giữa các điểm) với trọng số đại diện cho khoảng cách hoặc chi phí di chuyển giữa các đỉnh. Thuật toán hoạt động theo các bước sau:
Khởi Tạo
- Chọn một đỉnh bắt đầu và gán khoảng cách từ đỉnh này đến chính nó là 0.
- Gán khoảng cách từ đỉnh bắt đầu đến tất cả các đỉnh khác là vô cùng.
- Đánh dấu tất cả các đỉnh là chưa được thăm.
Thực Hiện
- Chọn đỉnh chưa được thăm có khoảng cách nhỏ nhất.
- Cập nhật khoảng cách cho các đỉnh kề cận bằng cách so sánh khoảng cách hiện tại với khoảng cách mới được tính thông qua đỉnh đang xét.
- Đánh dấu đỉnh đang xét là đã thăm.
- Lặp lại quá trình cho đến khi tất cả các đỉnh đã được thăm.
Kết Thúc
- Khi tất cả các đỉnh đã được thăm, khoảng cách từ đỉnh bắt đầu đến mỗi đỉnh sẽ đại diện cho khoảng cách ngắn nhất.
3. Ví Dụ Minh Họa
Giả sử chúng ta có một đồ thị đơn giản với các đỉnh A, B, C, D, và E, và các cạnh có trọng số như sau:
- A đến B: 4
- A đến C: 2
- B đến C: 5
- B đến D: 10
- C đến D: 3
- D đến E: 4
- C đến E: 7
Bắt đầu từ đỉnh A, chúng ta sẽ áp dụng thuật toán Dijkstra:
- Khởi tạo khoảng cách: A=0, B=∞, C=∞, D=∞, E=∞.
- Chọn A (khoảng cách nhỏ nhất = 0):
- Cập nhật: B=4, C=2.
- Đánh dấu A đã thăm.
- Chọn C (khoảng cách nhỏ nhất = 2):
- Cập nhật: D=5, E=9 (2 + 7).
- Đánh dấu C đã thăm.
- Chọn B (khoảng cách nhỏ nhất = 4):
- Không có cập nhật tốt hơn.
- Đánh dấu B đã thăm.
- Chọn D (khoảng cách nhỏ nhất = 5):
- Cập nhật: E=9 (5 + 4).
- Đánh dấu D đã thăm.
- Cuối cùng, tất cả các đỉnh đã được thăm, và ta có các khoảng cách ngắn nhất từ A đến các đỉnh còn lại.
4. Ứng Dụng Của Thuật Toán Dijkstra

Dr. Edsger Dijkstra at ETH Zurich in 1994 (image by Andreas F. Borchert)
Thuật toán Dijkstra có nhiều ứng dụng trong thực tế:
- Định Tuyến Mạng: Tìm đường đi ngắn nhất trong mạng máy tính.
- Điều Hướng GPS: Xác định tuyến đường ngắn nhất giữa hai địa điểm.
- Lập Kế Hoạch Robot: Giúp robot tìm đường đi tối ưu trong môi trường phức tạp.
- Quản Lý Giao Thông: Tối ưu hóa luồng giao thông bằng cách tính toán tuyến đường nhanh nhất.
Thuật toán Dijkstra là một công cụ mạnh mẽ và hiệu quả cho việc tìm đường ngắn nhất trong đồ thị, với nhiều ứng dụng quan trọng trong cuộc sống hàng ngày và các lĩnh vực công nghệ cao. Sự đơn giản và khả năng mở rộng của nó làm cho Dijkstra trở thành một trong những thuật toán cốt lõi trong khoa học máy tính.